题目内容
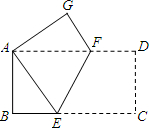 如图,将一个长为8cm,宽为4cm的长方形纸片ABCD折叠,使C点与A点重合,求GF的长.
如图,将一个长为8cm,宽为4cm的长方形纸片ABCD折叠,使C点与A点重合,求GF的长.分析:设GF=x,则BF=8-x,在Rt△BGF中利用勾股定理即可得出x的值.
解答:解:设BE=x,则AE=EC=8-x,在Rt△ABE中,
AE2=AB2+BE2
(8-x)2=42+x2
解得:x=3,
在△ABE和△AGF中,
∵
∴△ABE≌△AGF (ASA)
∴GF=BE=3(cm),
故GF的长为3cm.
AE2=AB2+BE2
(8-x)2=42+x2
解得:x=3,
在△ABE和△AGF中,
∵
|
∴△ABE≌△AGF (ASA)
∴GF=BE=3(cm),
故GF的长为3cm.
点评:本题考查了翻折变换,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
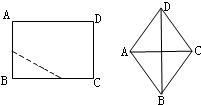
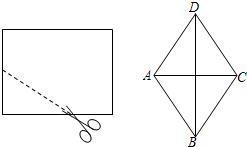 如图,将一个长为10cm,宽为8cm的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )
如图,将一个长为10cm,宽为8cm的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )| A、10cm2 | B、20cm2 | C、40cm2 | D、80cm2 |
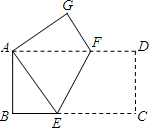 如图,将一个长为8cm,宽为4cm的长方形纸片ABCD折叠,使C点与A点重合,求GF的长.
如图,将一个长为8cm,宽为4cm的长方形纸片ABCD折叠,使C点与A点重合,求GF的长.