��Ŀ����
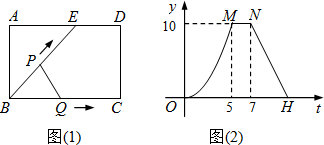
��2012•���ݣ���ͼ�ף��ı���OABC�ı�OA��OC�ֱ���x�ᡢy����������ϣ�������B��������߽�x���ڵ�A��D����y���ڵ�E������AB��AE��BE����֪tan��CBE=
��A��3��0����D��-1��0����E��0��3����
��1���������ߵĽ���ʽ������B�����ꣻ
��2����֤��CB�ǡ�ABE���Բ�����ߣ�
��3����̽�����������Ƿ����һ��P��ʹ��D��E��PΪ��������������ABE���ƣ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
��4�����AOE��x��������ƽ��t����λ���ȣ�0��t��3��ʱ����AOE���ABE�ص����ֵ����Ϊs����s��t֮��ĺ�����ϵʽ����ָ��t��ȡֵ��Χ��

| 1 | 3 |
��1���������ߵĽ���ʽ������B�����ꣻ
��2����֤��CB�ǡ�ABE���Բ�����ߣ�
��3����̽�����������Ƿ����һ��P��ʹ��D��E��PΪ��������������ABE���ƣ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
��4�����AOE��x��������ƽ��t����λ���ȣ�0��t��3��ʱ����AOE���ABE�ص����ֵ����Ϊs����s��t֮��ĺ�����ϵʽ����ָ��t��ȡֵ��Χ��

��������1����֪A��D��E��������꣬���ô���ϵ������ȷ�������ߵĽ���ʽ�������ܵõ�����B�����꣮
��2����B��BM��y����M����A��B��E�������꣬���жϳ���BME����AOE��Ϊ����ֱ�������Σ���֤�á�BEA=90�㣬����ABE��ֱ�������Σ���AB�ǡ�ABE���Բ��ֱ�������ֻ��֤��AB��CB��ֱ���ɣ�BE��AE���ã������tan��BAE��ֵ�����tan��CBE��ֵ���ɵõ���CBE=��BAE���ɴ�֤�á�CBA=��CBE+��ABE=��BAE+��ABE=90�㣬�����֤��
��3����ABE�У���AEB=90�㣬tan��BAE=
����AE=3BE������D��E��PΪ��������������ABE���ƣ���ô�������α���������������������һ������ֱ�ǡ�����ֱ�DZ�����1��3�ı�����ϵ��Ȼ������������⼴�ɣ�
��4����E��EF��x�ύAB��F����E���˶���EF֮��ʱ����AOE���ABE�ص������Ǹ��ı��Σ���E���˶���F���Ҳ�ʱ����AOE���ABE�ص������Ǹ������Σ����������������ͼ��֮��ĺͲ��ϵ������⣮
��2����B��BM��y����M����A��B��E�������꣬���жϳ���BME����AOE��Ϊ����ֱ�������Σ���֤�á�BEA=90�㣬����ABE��ֱ�������Σ���AB�ǡ�ABE���Բ��ֱ�������ֻ��֤��AB��CB��ֱ���ɣ�BE��AE���ã������tan��BAE��ֵ�����tan��CBE��ֵ���ɵõ���CBE=��BAE���ɴ�֤�á�CBA=��CBE+��ABE=��BAE+��ABE=90�㣬�����֤��
��3����ABE�У���AEB=90�㣬tan��BAE=
| 1 |
| 3 |
��4����E��EF��x�ύAB��F����E���˶���EF֮��ʱ����AOE���ABE�ص������Ǹ��ı��Σ���E���˶���F���Ҳ�ʱ����AOE���ABE�ص������Ǹ������Σ����������������ͼ��֮��ĺͲ��ϵ������⣮
�����1���⣺�����⣬�������߽���ʽΪy=a��x-3����x+1����
��E��0��3��������ʽ����ã�a=-1��
��y=-x2+2x+3��
���B��1��4����
 ��2��֤������ͼ1������B��BM��y�ڵ�M����M��0��4����
��2��֤������ͼ1������B��BM��y�ڵ�M����M��0��4����
��Rt��AOE��OA=OE=3��
���1=��2=45�㣬AE=
=3
��
��Rt��EMB��EM=OM-OE=1=BM��
���MEB=��MBE=45�㣬BE=
=
��
���BEA=180��-��1-��MEB=90�㣮
��AB�ǡ�ABE���Բ��ֱ����
��Rt��ABE��tan��BAE=
=
=tan��CBE��
���BAE=��CBE��
��Rt��ABE�У���BAE+��3=90�㣬���CBE+��3=90�㣮
���CBA=90�㣬��CB��AB��
��CB�ǡ�ABE���Բ�����ߣ�
��3���⣺Rt��ABE�У���AEB=90�㣬tan��BAE=
��sin��BAE=
��cos��BAE=
��
����D��E��PΪ��������������ABE���ƣ����DEP��Ϊֱ�������Σ�
��DEΪб��ʱ��P1��x���ϣ���ʱP1��O�غϣ�
��D��-1��0����E��0��3������OD=1��OE=3����tan��DEO=
=tan��BAE������DEO=��BAE
�����DEO�ס�BAE����������� O���Ƿ���������P1�㣬����Ϊ��0��0����
��DEΪ��ֱ�DZ�ʱ��P2��x���ϣ�
����D��E��PΪ��������������ABE���ƣ����DEP2=��AEB=90�㣬sin��DP2E=sin��BAE=
��
��DE=
=
����DP2=DE��sin��DP2E=
��
=10��OP2=DP2-OD=9
����P2��9��0����
��DEΪ��ֱ�DZ�ʱ����P3��y���ϣ�
����D��E��PΪ��������������ABE���ƣ����EDP3=��AEB=90�㣬cos��DEP3=cos��BAE=
��
��EP3=DE��cos��DEP3=
��
=
��OP3=EP3-OE=
��
���ϣ��ã�P1��0��0����P2��9��0����P3��0��-
����
��4���⣺��ֱ��AB�Ľ���ʽΪy=kx+b��
��A��3��0����B��1��4�����룬��
�����
��
��y=-2x+6��
����E������EF��x�ύAB�ڵ�F����y=3ʱ����x=
����F��
��3����
 ���һ����ͼ2����0��t��
���һ����ͼ2����0��t��
ʱ�����AOEƽ�Ƶ���GNM��λ�ã�MG��AB�ڵ�H��MN��AE�ڵ�S��
��ON=AG=t������H��LK��x���ڵ�K����EF�ڵ�L��
�ɡ�AHG�ס�FHM����
=
����
=
��
���HK=2t��
��S��=S��MNG-S��SNA-S��HAG=
��3��3-
��3-t��2-
t•2t=-
t2+3t��
 ���������ͼ3����
���������ͼ3����
��t��3ʱ�����AOEƽ�Ƶ���PQR��λ�ã�PQ��AB�ڵ�I����AE�ڵ�V��
�ɡ�IQA�ס�IPF����
=
����
=
��
���IQ=2��3-t����
��AQ=VQ=3-t��
��S��=
IV•AQ=
��3-t��2=
t2-3t+
��
����������s=
��
��E��0��3��������ʽ����ã�a=-1��
��y=-x2+2x+3��
���B��1��4����
 ��2��֤������ͼ1������B��BM��y�ڵ�M����M��0��4����
��2��֤������ͼ1������B��BM��y�ڵ�M����M��0��4������Rt��AOE�У�OA=OE=3��
���1=��2=45�㣬AE=
| OA2+OE2 |
| 2 |
��Rt��EMB��EM=OM-OE=1=BM��
���MEB=��MBE=45�㣬BE=
| EM2+BM2 |
| 2 |
���BEA=180��-��1-��MEB=90�㣮
��AB�ǡ�ABE���Բ��ֱ����
��Rt��ABE��tan��BAE=
| BE |
| AE |
| 1 |
| 3 |
���BAE=��CBE��
��Rt��ABE�У���BAE+��3=90�㣬���CBE+��3=90�㣮
���CBA=90�㣬��CB��AB��
��CB�ǡ�ABE���Բ�����ߣ�
��3���⣺Rt��ABE�У���AEB=90�㣬tan��BAE=
| 1 |
| 3 |
| ||
| 10 |
3
| ||
| 10 |
����D��E��PΪ��������������ABE���ƣ����DEP��Ϊֱ�������Σ�
��DEΪб��ʱ��P1��x���ϣ���ʱP1��O�غϣ�
��D��-1��0����E��0��3������OD=1��OE=3����tan��DEO=
| 1 |
| 3 |
�����DEO�ס�BAE����������� O���Ƿ���������P1�㣬����Ϊ��0��0����
��DEΪ��ֱ�DZ�ʱ��P2��x���ϣ�
����D��E��PΪ��������������ABE���ƣ����DEP2=��AEB=90�㣬sin��DP2E=sin��BAE=
| ||
| 10 |
��DE=
| 12+32 |
| 10 |
| 10 |
| ||
| 10 |
����P2��9��0����
��DEΪ��ֱ�DZ�ʱ����P3��y���ϣ�
����D��E��PΪ��������������ABE���ƣ����EDP3=��AEB=90�㣬cos��DEP3=cos��BAE=
3
| ||
| 10 |
��EP3=DE��cos��DEP3=
| 10 |
3
| ||
| 10 |
| 10 |
| 3 |
| 1 |
| 3 |
���ϣ��ã�P1��0��0����P2��9��0����P3��0��-
| 1 |
| 3 |
��4���⣺��ֱ��AB�Ľ���ʽΪy=kx+b��
��A��3��0����B��1��4�����룬��
|
|
��y=-2x+6��
����E������EF��x�ύAB�ڵ�F����y=3ʱ����x=
| 3 |
| 2 |
| 3 |
| 2 |
 ���һ����ͼ2����0��t��
���һ����ͼ2����0��t��| 3 |
| 2 |
��ON=AG=t������H��LK��x���ڵ�K����EF�ڵ�L��
�ɡ�AHG�ס�FHM����
| AG |
| FM |
| HK |
| HL |
| t | ||
|
| HK |
| 3-HK |
���HK=2t��
��S��=S��MNG-S��SNA-S��HAG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
 ���������ͼ3����
���������ͼ3����| 3 |
| 2 |
�ɡ�IQA�ס�IPF����
| AQ |
| FP |
| IQ |
| IP |
| 3-t | ||
t-
|
| IQ |
| 3-IQ |
���IQ=2��3-t����
��AQ=VQ=3-t��
��S��=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
����������s=
|
���������⿼���˶��κ������ۺ��⣬�漰�����κ�������ʽ��ȷ�������ߵ��ж������������ε��ж���ͼ������Ľⷨ���ص�֪ʶ���ۺ���ǿ���Ѷ�ϵ���ϴ�����ѵ����ں�����С�⣬���Ƕ���Ҫ������������ۣ����׳���©���������ڽ����ĺ�������ʱ��һ����Ҫ��©��Ӧ���Ա���ȡֵ��Χ��

��ϰ��ϵ�д�
�����Ŀ
 ��2012•���ݣ���ͼ����ABC�ǵȱ������Σ�P�ǡ�ABC��ƽ����BD��һ�㣬PE��AB�ڵ�E���߶�BP�Ĵ�ֱƽ���߽�BC�ڵ�F������Ϊ��Q����BF=2����PE�ij�Ϊ��������
��2012•���ݣ���ͼ����ABC�ǵȱ������Σ�P�ǡ�ABC��ƽ����BD��һ�㣬PE��AB�ڵ�E���߶�BP�Ĵ�ֱƽ���߽�BC�ڵ�F������Ϊ��Q����BF=2����PE�ij�Ϊ�������� ��2012•���ݣ���ͼ����ֱ������ϵ�У��ı���OABC��ֱ�����Σ�BC��OA����P�ֱ���OA��OC��BC�����ڵ�E��D��B����AB���ڵ�F����֪A��2��0����B��1��2������tan��FDE=
��2012•���ݣ���ͼ����ֱ������ϵ�У��ı���OABC��ֱ�����Σ�BC��OA����P�ֱ���OA��OC��BC�����ڵ�E��D��B����AB���ڵ�F����֪A��2��0����B��1��2������tan��FDE= ��2012•���ݣ���ͼ��һ�����µ��ܷ�ֽ�е�����ͼ���������ͼ�����ݣ���������ܷ�ֽ�еı����Ϊ
��2012•���ݣ���ͼ��һ�����µ��ܷ�ֽ�е�����ͼ���������ͼ�����ݣ���������ܷ�ֽ�еı����Ϊ