题目内容
【题目】阅读材料：
在一个三角形中，各边和它所对角的正弦的比相等，
，利用上述结论可以求解如下题目：
在△ABC中，∠A、∠B、∠C的对边分别为a，b，c．若∠A=45°，∠B=30°，a=6，求b．
解：在△ABC中，∵
，∴
．
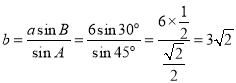理解应用：
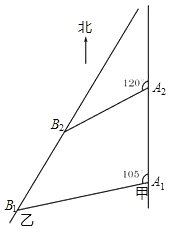
如图，甲船以每小时
海里的速度向正北方向航行，当甲船位于A1处时，乙船位于甲船的北偏西105°方向的B1处，且乙船从B1处按北偏东15°方向匀速直线航行，当甲船航行20分钟到达A2时，乙船航行到甲船的北偏西120°方向的B2处，此时两船相距
海里．
（1）判断△A1A2B2的形状，并给出证明；
（2）求乙船每小时航行多少海里？
【答案】（1）等边三角形；（2）
．
【解析】
试题分析：（1）先根据路程=速度×时间求出A1A2的长，又A2B2=
，∠A1A2B2=60°，根据有一个角是60°的等腰三角形是等边三角形即可得出△A1A2B2是等边三角形；
（2）先由平行线的性质及方向角的定义求出∠A1B1B2=75°﹣15°=60°，由等边三角形的性质得出∠A2A1B2=60°，A1B2=A1A2=，那么∠B1A1B2=105°﹣60°=45°．然后在△B1A1B2中，根据阅读材料可知，
，求出B1B2的距离，再由时间求出乙船航行的速度．
试题解析：解：（1）△A1A2B2是等边三角形，理由如下：
连结A1B2．∵甲船以每小时
海里的速度向正北方向航行，航行20分钟到达A2，∴A1A2=×
=，又∵A2B2=，∠A1A2B2=60°，∴△A1A2B2是等边三角形；
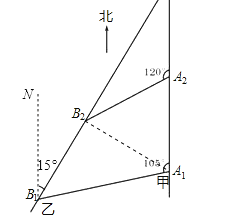
（2）如图，∵B1N∥A1A2，∴∠A1B1N=180°﹣∠B1A1A2=180°﹣105°=75°，∴∠A1B1B2=75°﹣15°=60°．∵△A1A2B2是等边三角形，∴∠A2A1B2=60°，A1B2=A1A2=，∴∠B1A1B2=105°﹣60°=45°．在△B1A1B2中，∵A1B2=，∠B1A1B2=105°﹣60°=45°，∠A2A1B2=60°，由阅读材料可知，，解得B1B2=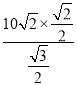
=
，所以乙船每小时航行：
=海里．
