��Ŀ����
��֪���κ���ͼ��Ķ�������ΪM��1��0����ֱ��y=x+m��ö��κ�����ͼ����A��B���㣬����A�������Ϊ��3��4����B����y���ϣ�
��1����m��ֵ��������κ����Ľ���ʽ��
��2����x������һ��Q��ʹ��QAB���ܳ���С���������ʱQ�����ꣻ
��3����P��a��0����x���ϵ�һ�����㣬��P��x��Ĵ��߷ֱ���ֱ��AB�Ͷ��κ�����ͼ����D��E���㣮
�����߶�DE�ij�Ϊh����0��a��3ʱ����h��a֮��ĺ�����ϵʽ��
����ֱ��AB�������ߵĶԳ��ύ��ΪN�����Ƿ����һ��P��ʹ��M��N��D��EΪ������ı�����ƽ���ı���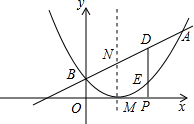 �������ڣ��������ʱP������ꣻ�������ڣ���˵�����ɣ�
�������ڣ��������ʱP������ꣻ�������ڣ���˵�����ɣ�
�⣺��1���������ߵĽ���ʽΪy=a��x-1��2��
�ߵ�A��3��4�����������ϣ���4=a��3-1��2��
���a=1��
�������ߵĽ���ʽΪy=��x-1��2
�ߵ�A��3��4��Ҳ��ֱ��y=x+m����4=3+m��
���m=1��
��2��ֱ��y=x+1��y��Ľ���B������ΪB��0��1����
B�����x��ĶԳƵ�B��������ΪB�䣨0��-1����
��ֱ��AB��Ľ���ʽΪy=kx+b��
��A��B�������������y=kx+b��
���k= ��b=-1��
��b=-1��
����ֱ��AB�Ľ���ʽΪy= x-1��
x-1��
��A��Q��B��������һ��ֱ����ʱ��
AQ+BQ��ֵ��С������QAB���ܳ���С��
Q�㼴Ϊֱ��AB����x��Ľ��㣮
Q������Ϊ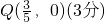
��3������֪P������ΪP��a��0������E������ΪE��a��a2-2a+1����D������ΪD��a��a+1����
h=DE=yD-yE=a+1-��a2-2a+1��=-a2+3a��
��h��a֮��ĺ�����ϵʽΪh=-a2+3a��0��a��3��
�ڴ���һ��P��ʹ��M��N��D��EΪ������ı�����ƽ���ı���
�����ǡ�M��1��0����
���x=1����y=x+1�ã�y=2��
��N��1��2����
��MN=2��
Ҫʹ�ı���NMED��ƽ���ı��Σ�����DE=MN=2��
�ɢ�֪DE=|-a2+3a|��
��2=|-a2+3a|��
��ã�a1=2��a2=1��a3= ��a4=
��a4= ��
��
�ࣨ2��0������1��0������Ϊ��M�غϣ���ȥ���� ��0������
��0������ ��0��
��0��
��P�������ǣ�2��0������ ��0������
��0������ ��0����
��0����
��������1����A������ֱ���������ߵ�ֱ�ߣ������������ߵĽ���ʽ��m��ֵ��
��2��ʹ��QAB���ܳ���С��������AQ+BQ��ֵ��С������B�����x��ĶԳƵ�B�䣬��A��Q��B��������һ��ֱ����ʱ����QAB���ܳ���С��
��3���ٸ���P������ֱ����DE�������꣬������h��a֮��ĺ�����ϵʽ��
�ڴ��ڣ�P������Ϊ�� ��0������
��0������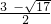 ��0����
��0����
�����������Ƕ��κ������ۺ��⣬�����漰����֪ʶ���������ߵĹ�ʽ���������ε����ʵ�֪ʶ�㣬�Ǹ����п����ȵ���ѵ㣬����ʱע�����ν����ѧ˼������ã�ͬѧ��Ҫ��ǿѵ���������е��⣮
�ߵ�A��3��4�����������ϣ���4=a��3-1��2��
���a=1��
�������ߵĽ���ʽΪy=��x-1��2
�ߵ�A��3��4��Ҳ��ֱ��y=x+m����4=3+m��
���m=1��
��2��ֱ��y=x+1��y��Ľ���B������ΪB��0��1����
B�����x��ĶԳƵ�B��������ΪB�䣨0��-1����
��ֱ��AB��Ľ���ʽΪy=kx+b��
��A��B�������������y=kx+b��
���k=
 ��b=-1��
��b=-1������ֱ��AB�Ľ���ʽΪy=
 x-1��
x-1����A��Q��B��������һ��ֱ����ʱ��
AQ+BQ��ֵ��С������QAB���ܳ���С��
Q�㼴Ϊֱ��AB����x��Ľ��㣮
Q������Ϊ
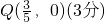
��3������֪P������ΪP��a��0������E������ΪE��a��a2-2a+1����D������ΪD��a��a+1����
h=DE=yD-yE=a+1-��a2-2a+1��=-a2+3a��
��h��a֮��ĺ�����ϵʽΪh=-a2+3a��0��a��3��
�ڴ���һ��P��ʹ��M��N��D��EΪ������ı�����ƽ���ı���
�����ǡ�M��1��0����
���x=1����y=x+1�ã�y=2��
��N��1��2����
��MN=2��
Ҫʹ�ı���NMED��ƽ���ı��Σ�����DE=MN=2��
�ɢ�֪DE=|-a2+3a|��
��2=|-a2+3a|��
��ã�a1=2��a2=1��a3=
 ��a4=
��a4= ��
���ࣨ2��0������1��0������Ϊ��M�غϣ���ȥ����
 ��0������
��0������ ��0��
��0����P�������ǣ�2��0������
 ��0������
��0������ ��0����
��0������������1����A������ֱ���������ߵ�ֱ�ߣ������������ߵĽ���ʽ��m��ֵ��
��2��ʹ��QAB���ܳ���С��������AQ+BQ��ֵ��С������B�����x��ĶԳƵ�B�䣬��A��Q��B��������һ��ֱ����ʱ����QAB���ܳ���С��
��3���ٸ���P������ֱ����DE�������꣬������h��a֮��ĺ�����ϵʽ��
�ڴ��ڣ�P������Ϊ��
 ��0������
��0������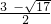 ��0����
��0���������������Ƕ��κ������ۺ��⣬�����漰����֪ʶ���������ߵĹ�ʽ���������ε����ʵ�֪ʶ�㣬�Ǹ����п����ȵ���ѵ㣬����ʱע�����ν����ѧ˼������ã�ͬѧ��Ҫ��ǿѵ���������е��⣮

��ϰ��ϵ�д�
 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д�
�����Ŀ
�з��̻����Ӧ���⣺�ҹ���һ������ˮ��Դȱ���Ĺ��ң�Ϊ�˹��������Լ��ˮ��ij�г���ˮ�Ѱ��±��涨��ȡ��ѧ����ΰ�����·ݹ���ˮ��17Ԫ���������·���ˮ���ٶ֣�
| ÿ��ÿ����ˮ�� | ������10�֣���10�֣� | ����10�ֵIJ��� |
| ˮ�ѵ��� | 1.30Ԫ/�� | 2.00Ԫ/�� |
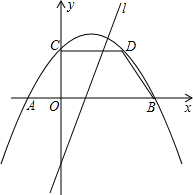 ��ͼ��������y=ax2+bx+c����ֱ��x=1�Գƣ��������ύ��A��B��C���㣬��AB=4����D��2��
��ͼ��������y=ax2+bx+c����ֱ��x=1�Գƣ��������ύ��A��B��C���㣬��AB=4����D��2�� �����������ϣ�ֱ��l��һ�κ���y=kx-2��k��0����ͼ��O������ԭ�㣮
�����������ϣ�ֱ��l��һ�κ���y=kx-2��k��0����ͼ��O������ԭ�㣮 ����AB=2
����AB=2 ��AO=4��
��AO=4��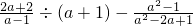 ����2��
����2��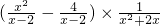 ��
��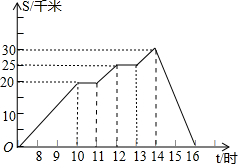 ��ʱ���Ĺ�ϵ��ͼ�е�������ʾ���������ͼ��ش��������⣺
��ʱ���Ĺ�ϵ��ͼ�е�������ʾ���������ͼ��ش��������⣺