题目内容
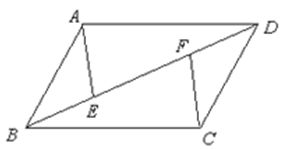
如图, △ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
(1)证明见解析;(2)∠BAC=90°
试题分析:(1)利用平行四边形的判定首先得出四边形AEBD是平行四边形,进而理由等腰三角形的性质得出∠ADB=90°,即可得出答案;
(2)利用等腰直角三角形的性质得出AD=BD=CD,进而利用正方形的判定得出即可.
试题解析:(1)O是AB中点,
∴OA=OB
OE=OD
∴四边形AEBD是平行四边形
又∵AB=AC
AD是△ABC的角平分线
∴AD⊥BC
∴平行四边形AEBD是矩形
(2)当∠BAC=90°时,矩形AEBD是正方形
∵∠BAC=90°
又∵AB=AC
AD是△ABC的角平分线
∴BD=CD
∴AD=BD
∴矩形AEBD是正方形
考点: 1.正方形的判定;2.矩形的判定.

练习册系列答案
相关题目


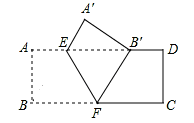
 中,
中,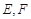 是对角线
是对角线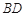 上的两点,且
上的两点,且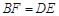 .求证:
.求证: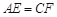 .
.