题目内容
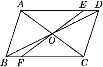
【题目】如图1,在数轴上A,B两点对应的数分别是6,-6,∠DCE=90°(C与O重合,D点在数轴的正半轴上)
(1)如图1,若CF平分∠ACE,则∠AOF=_______;
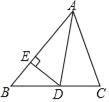
(2)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α.
①当t=1时,α=_______
②猜想∠BCE和α的数量关系,并证明;
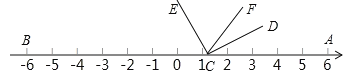
(3)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0<t<3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α-β|=40°,请直接写出t的值为

【答案】(1)45°;(2)①30°;②∠BCE=2α,理由见解析;(3)![]()
【解析】
(1)根据角平分线的定义计算即可;
(2)①根据∠FCD=∠ACF-∠ACD,求出∠ACF,∠ACD即可;
②猜想:∠BCE=2α.根据∠BCE=∠AOB-∠ECD-∠ACD计算即可;
(3)求出α,β(用t表示),构建方程即可解决问题;
解:(1)如图1中,

∵∠EOD=90°,OF平分∠EOD,
∴∠FOD=![]() ∠EOD=45°,
∠EOD=45°,
故答案为:45°;
(2)①如下图,
当t=1时,∵∠DCA=30°,∠ECD=90°,
∴∠ECA=120°,
∵CF平分∠ACE,
∴∠FCA=![]() ∠ECA=60°
∠ECA=60°
∴α=∠FCD=60°-30°=30°
故答案为:30°.
②如下图,猜想:∠BCE=2α.

理由:∵∠DCE=90°,∠DCF=α,
∴∠ECF=90°-α,
∵CF平分∠ACE,
∴∠ACF=∠ECF=90°-α,
∵点A,O,B共线
∴∠AOB=180°
∴∠BCE=∠AOB-∠ECD-∠ACD=180°-90°-(90°-2α)=2α.
(3)如图3中,
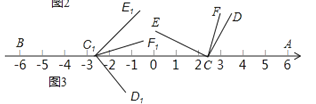
由题意:α=∠FCA-∠DCA=![]() (90°+30t)-30t=45°-15t,
(90°+30t)-30t=45°-15t,
β=∠AC1D1+∠AC1F1=30t+![]() (90°-30t)=45°+15t,
(90°-30t)=45°+15t,
∵β-α=40°,
∴30t=40°,
解得:t=![]() .
.
故答案为:![]() .
.

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案【题目】某体育用品商场采购员要到厂家批发购进篮球和排球共100个,付款总额不得超过11815元.已知:厂家两种球的批发价如(表![]() )、商场在某两天的零售信息如(表
)、商场在某两天的零售信息如(表![]() ):
):
品名 | 厂家批发价(元/个) |
篮球 | 130 |
排球 | 100 |
(表![]() )
)
篮球(个) | 排球(个) | 零售总价(元) | |
第一天 | 8 | 5 | 1880 |
第二天 | 6 | 10 | 2160 |
(表![]() )
)
请解决以下问题:
(1)求出体育商场出售篮球和排球的零售单价.
(2)该采购员最多可从厂家购进篮球多少个.
(3)若该商场把这100个球全部以零售价售出,为使商场的利润不低于2580元,则采购员采购的方案有哪几种?该商场最多可盈利__________元.