Question

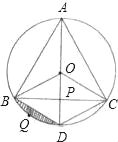
【题目】等边三角形ABC内接于⊙O，连接OA，OB，OC，延长AO分别交BC于点P，弧BC于点D，连接BD，CD．

（1）判断四边形BDCO是哪一种特殊四边形，并说明理由；

（2）若等边三角形ABC的边长6cm，求⊙O的半径；

（3）在劣弧BD上有一点Q，请求出弓形BQD的面积．

Answer 1

【答案】（1）四边形BDCO是菱形理由见解析；（2）6；（3）6π-9 ．

【解析】

（1）可先由四边形各角的大小求出各边之间的关系，然后即可判断四边形BDCO为何种特殊四边形；

（2）先由菱形性质求出BP的长，再由等边三角形性质及求出∠POB的角度，然后即可由三角形边角关系求出OB的长，即⊙O的半径；

（3）弓形BQD的面积可由求扇形OBD与三角形OBD之差间接求得．

解：（1）四边形BDCO是菱形，理由如下：

∵AB＝BC＝AC，

∴∠AOB＝∠BOC＝∠COA＝120°，

∴∠BOD＝180°﹣∠AOB＝60°，

∴∠COD＝180°﹣∠AOC＝60°；

又∵OB＝OD，

∴△OBD为正三角形，

∴OB＝OD＝BD

同理可得OC＝CD，

∴OB＝OC＝BO＝CD即四边形BDCO是菱形；

（2）由菱形性质可知，BP=BC=×6 =3；

∵△ABC为等边三角形，∠PBO＝30°，OP＝3，BO＝6，

∴⊙O的半径OB为6．

（3）S弓形BQD=S扇形-S△BOD=××62 ＝6π-9 ．