Question

【题目】已知AB∥CD，在AB，CD内有一条折线EGF．

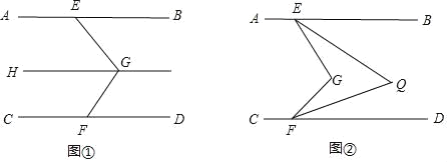
（1）如图①，过点G作GH∥AB，求证：∠BEG+∠DFG＝∠EGF；

（2）如图②，已知∠BEG的平分线与∠DFG的平分线相交于点Q，请探究∠EGF与∠EQF的数量关系，并说明理由．

Answer 1

【答案】（1）见解析；（2）∠EQF＝∠EGF，理由见解析

【解析】

（1）根据平行线的性质，两直线平行，内错角相等，即可得出∠EGH＝∠BEG，∠DFG＝∠FGH，即可得证；

（2）由（1）的结论得出∠EGF＝∠BEG+∠DFG，∠EQF＝∠BEQ+∠DFQ，然后由角平分线的性质得出∠DFQ＝∠ DFG，∠BEQ＝ ∠BEG，，进而得出∠EQF＝∠EGF.

（1）∵GH∥AB，AB∥CD，

∴GH∥CD，

∴∠EGH＝∠BEG，∠DFG＝∠FGH，

∵∠EGF＝∠EGH+∠FGH，

∴∠BEG+∠DFG＝∠EGF

（2）由（1）知，∠EGF＝∠BEG+∠DFG，∠EQF＝∠BEQ+∠DFQ，

∵EQ，FQ分别平分∠BEG，∠DFG，

∴∠DFQ＝∠ DFG，∠BEQ＝ ∠BEG，

∴∠EQF＝ （∠BEG+∠DFG）＝ ∠EGF