题目内容
【题目】如图,将△ABC绕点B按逆时针方向旋转得到△EBD,点E、点D分别与点A、点C对应,且点D在边AC上,边DE交边AB于点F,△BDC∽△ABC.已知BC= ![]() ,AC=5,那么△DBF的面积等于 .
,AC=5,那么△DBF的面积等于 . 
【答案】![]()
【解析】解:∵△BDC∽△ABC, ∴ ![]() ,∠CBD=∠A,
,∠CBD=∠A,
∴CD= ![]() ,
,
∵BC= ![]() ,AC=5,
,AC=5,
∴CD=2,
∴AD=3,
∵将△ABC绕点B按逆时针方向旋转得到△EBD,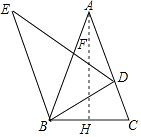
∴∠ABC=∠EBD,∠E=∠A,AB=BE,DE=AC,
∴∠EBF=∠CBD,
∴∠EBF=∠A,
∴BE∥AC,
∴∠ADF=∠E,
∴∠E=∠EBF=∠A=∠ADF,
∴EF=BF,AF=DF,
∴AF+BF=EF+DF,
即AB=DE=AC=5,
∵AD∥BE,
∴△ADF∽△BEF,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
过A 作AH⊥BC于H,
∴AH= ![]() =
= ![]() ,
,
∵S△BDE=S△ABC= ![]() ×
× ![]() ×
× ![]() =
= ![]() ,
,
∴△DBF的面积= ![]() S△ABC=
S△ABC= ![]() .
.
所以答案是: ![]() .
.
【考点精析】本题主要考查了相似三角形的性质和旋转的性质的相关知识点,需要掌握对应角相等,对应边成比例的两个三角形叫做相似三角形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目







