题目内容
如下图,正方形ABCD中,G是CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE,连接BG并延长交DE于H。
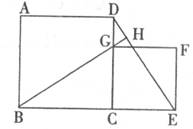
(1)求证:∠BGC=∠DEC。
(2)若正方形ABCD的边长为1,试问当点G运动到什么位置时,BH垂直平分DE?
(1)证明:∵四边形ABCD、GCEF都是正方形,
∴BC=DC,∠BCG=∠DCE=90°,GC=EC
∴.△BCG≌△DCE
∴∠BGC=∠DEC
(2)解:连接BD
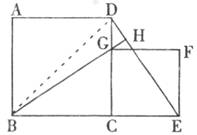
如果BH垂直平分DE,则有BD=BE
∵BC=CD=1,∴BD=![]()
∴CE=BE-BC=![]() -1
-1
∴CG=CE=![]() -1
-1
即当CG=![]() -1时,BH垂直平分DE
-1时,BH垂直平分DE

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目