题目内容
解答题
(1)已知![]() +a=3,求
+a=3,求![]() +a2的值.
+a2的值.
(2)已知a+b=5,ab=-10,求下列各式的值:
①a2+b2;②(a-b)2.
答案:
解析:
解析:
|
解 (1)将 ( 又 ( 所以 (2)①因为(a+b)2=a2+2ab+b2, 所以 a2+b2=(a+b)2-2ab, 又 a+b=5,ab=-10, 所以 a2+b2=52-2×(-10)=25+20=45. ②因为ab=-10,又由①,a2+b2=45,所以 (a-b)2=a2+b2-2ab =45-2×(-10)=45+20=65. 或因为(a-b)2=(a+b)2-4ab,又a+b=5,ab=-10, 所以(a-b)2=52-4×(-10)=25+40=65. 分析 (1)题中由于( (2)题由于(a+b)2=a2+2ab+b2,可得a2+b2=(a+b)2-2ab,则可求得①中的a2+b2的值;而②中的(a-b)2=a2+b2-2ab利用①代入便可求值;或由于(a-b)2=(a+b)2-4ab,利用条件代入也可. |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 说理解答题
说理解答题
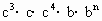 ,计算
,计算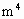 .
.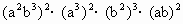 .
.