题目内容
如图，过点Q（0，3.5）的一次函数与正比例函数y=2x的图象相交于横坐标为1的点P，能表示这个一次函数图象的方程式是
- A.3x+2y+7=0
- B.3x-2y-7=0
- C.3x+2y-7=0
- D.y=3x-7
C
分析：把横坐标1代入正比例函数解析式求出点P的坐标，然后利用待定系数法求一次函数解析式计算即可．
解答：∵点P的横坐标为1，
∴y=2×1=2，
∴点P的坐标为（1，2），
设一次函数解析式为y=kx+b，
则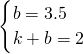
，
解得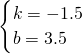
，
∴这个一次函数解析式为y=-1.5x+3.5，
即3x+2y-7=0．
故选C．
点评：本题考查了两直线相交的问题，根据点在直线上的特点求出点P的坐标是解题的关键．
分析：把横坐标1代入正比例函数解析式求出点P的坐标，然后利用待定系数法求一次函数解析式计算即可．
解答：∵点P的横坐标为1，
∴y=2×1=2，
∴点P的坐标为（1，2），
设一次函数解析式为y=kx+b，
则
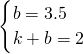，解得
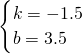，∴这个一次函数解析式为y=-1.5x+3.5，
即3x+2y-7=0．
故选C．
点评：本题考查了两直线相交的问题，根据点在直线上的特点求出点P的坐标是解题的关键．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
8、如图，过点P画出射线PM，PN，使PM∥OA，PN∥OB，且射线PM和射线OA，射线PN和射线OB方向分别相同，量一量∠O和∠P，你能得到什么结论？如果射线PM和射线OA，射线PN和射线OB一组方向相同、另一组方向相反，∠O和∠P又有什么关系呢？如果两组方向都相反，∠O和∠P有什么关系？
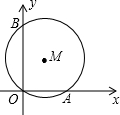如图，过点O、A（1，0）、B（0，| 3 |
| A、60° |
| B、60°或120° |
| C、30° |
| D、30°或150° |
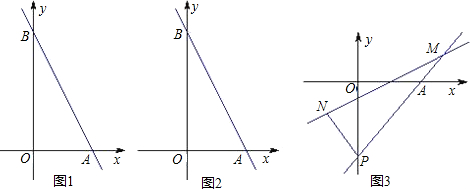
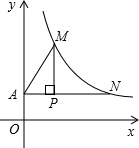如图，过点P（2，
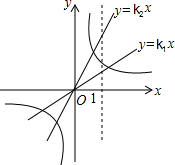如图，过点A（1，0）的直线与y轴平行，且分别与正比例函数y=k1x，y=k2x和反比例