Question

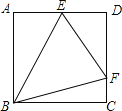
【题目】如图，在正方形ABCD中，E、F分别是边AD、CD上的点，∠EBF=45°，△EDF的周长为8，则正方形ABCD的边长为（ ）

A．2 B．3 C．5 D．4

Answer 1

【答案】D

【解析】解：∵四边形ABCD为正方形，

∴AB=BC，∠BAE=∠C=90°，

∴把△ABE绕点A顺时针旋转90°可得到△BCG，如图，

∴BG=BE，CG=AE，∠GBE=90°，∠BAE=∠C=90°，

∴点G在DC的延长线上，

∵∠EBF=45°，

∴∠FBG=∠EBG﹣∠EBF=45°，

∴∠FBG=∠FBE，

在△FBG和△EBF中，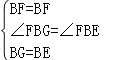

∴△FBG≌△EBF（SAS），

∴FG=EF，

而FG=FC+CG=CF+AE，

∴EF=CF+AE，

∵△DEF的周长=DF+DE+CF+AE=CD+AD=8，

∴AD=4；

故选：D．