题目内容
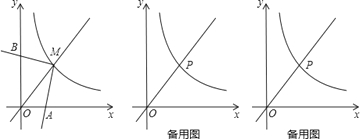
【题目】如图,反比例函数y=![]() (x>0)的图象与直线y=x交于点M,∠AMB=90°,其两边分别与两坐标轴的正半轴交于点A,B,四边形OAMB的面积为6.
(x>0)的图象与直线y=x交于点M,∠AMB=90°,其两边分别与两坐标轴的正半轴交于点A,B,四边形OAMB的面积为6.
(1)求k的值;
(2)点P在反比例函数y=![]() (x>0)的图象上,若点P的横坐标为3,∠EPF=90°,其两边分别与x轴的正半轴,直线y=x交于点E,F,问是否存在点E,使得PE=PF?若存在,求出点E的坐标;若不存在,请说明理由.
(x>0)的图象上,若点P的横坐标为3,∠EPF=90°,其两边分别与x轴的正半轴,直线y=x交于点E,F,问是否存在点E,使得PE=PF?若存在,求出点E的坐标;若不存在,请说明理由.
【答案】(1)6;(2)E(4,0)或E(6,0).
【解析】试题分析:(1)过点M作MC⊥x轴于点C,MD⊥y轴于点D,根据AAS证明△AMC≌△BMD,那么S四边形OCMD=S四边形OAMB=6,根据反比例函数比例系数k的几何意义得出k=6;
(2)先根据反比例函数图象上点的坐标特征求得点P的坐标为(3,2).再分两种情况进行讨论:①如图2,过点P作PG⊥x轴于点G,过点F作FH⊥PG于点H,交y轴于点K.根据AAS证明△PGE≌△FHP,进而求出E点坐标;②如图3,同理求出E点坐标.
试题解析:(1)如图1,过点M作MC⊥x轴于点C,MD⊥y轴于点D,

则∠MCA=∠MDB=90°,∠AMC=∠BMD,MC=MD,
∴△AMC≌△BMD,
∴S四边形OCMD=S四边形OAMB=6,
∴k=6;
(2)存在点E,使得PE=PF.
由题意,得点P的坐标为(3,2).
①如图2,过点P作PG⊥x轴于点G,过点F作FH⊥PG于点H,交y轴于点K.
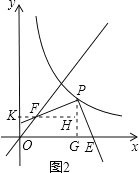
∵∠PGE=∠FHP=90°,∠EPG=∠PFH,PE=PF,
∴△PGE≌△FHP,
∴PG=FH=2,FK=OK=3-2=1,GE=HP=2-1=1,
∴OE=OG+GE=3+1=4,
∴E(4,0);
②如图3,过点P作PG⊥x轴于点G,过点F作FH⊥PG于点H,交y轴于点K.
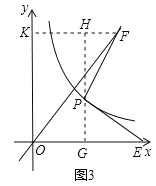
∵∠PGE=∠FHP=90°,∠EPG=∠PFH,PE=PF,
∴△PGE≌△FHP,
∴PG=FH=2,FK=OK=3+2=5,GE=HP=5-2=3,
∴OE=OG+GE=3+3=6,
∴E(6,0).

 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案