题目内容
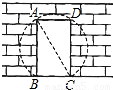
为美化校园，学校决定将花园边墙上的矩形门ABCD改为以AC为直径的圆弧形门，如图所示，量得矩形门宽为1m，对角线AC的长为2m．
（1）求原矩形门的面积；
（2）求要打掉的墙体面积．（结果保留л和根号）
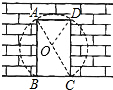解：（1）∵在Rt△ADC中，AD=1，AC=2，根据勾股定理得：DC=
=
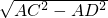m，∴S矩形ABCD=AD•DC=
m2；（2）由直径AC=2m，得到半径OA=OC=OD=1m，
∵sin∠ACD=
=
，∴∠ACD=30°，
则∠AOD=60°，
则S△AOD=
，S扇形AOD=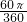
=
，则S弓形BC=S弓形AD=
-则S打掉墙体=S圆O-S矩形ABCD-S弓形BC=π-
-+=
-
．分析：（1）在直角三角形ADC中，由AD与AC的长，利用勾股定理求出DC的长，然后利用矩形的面积=长×宽，即可求出矩形ABCD的面积；
（2）打掉墙体的面积=圆O的面积-矩形ABCD的面积，求出即可．
点评：此题考查了垂径定理的应用，勾股定理，等边三角形的性质，以及扇形的面积公式，熟练掌握定理及性质是解本题的关键．
练习册系列答案
相关题目
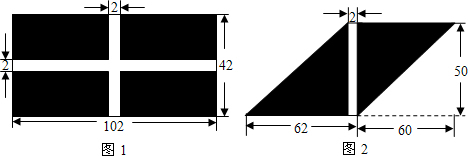
为了参加市教委举行的“争创绿色学校，美化校园环境”的活动，某区教委决定委托园林公司对所辖甲、乙两所学校进行校园绿化工作．已知甲校有如图1所示的矩形内阴影部分空地需铺设草坪，乙校有如图2所示的平行四边形内阴影部分空地需铺设草坪（图1，图2中数据单位均为“米”）．在A、B两地分别有同种草皮4500米2和2500米2出售，且售价一样．若园林公司向A、B两地购买草皮，其路程和运费单价表如下：
（注：运费单价表示每平方米草皮运送1千米所需要的人民币）
（1）分别求出图1、图2的阴影部分面积；
（2）若甲校从A地购买x米2的草皮（x取整数），因路程关系，甲校从A地购买的草皮数不超过甲校从B地购买的草皮数，乙校从B地购买的草皮数大于甲校从B地购买的草皮数的
，那么甲校乙校从A，B两地购买草皮的方案有多少种？
（3）在（2）的条件下，请你设计出总运费最低的草皮运送方案，并说明理由．
| 甲校 | 乙校 | |||
| 路程（千米） | 运费单价（元） | 路程（千米） | 运费单价（元） | |
| A地 | 20 | 0.3 | 10 | 0.3 |
| B地 | 15 | 0.2 | 20 | 0.2 |
（1）分别求出图1、图2的阴影部分面积；
（2）若甲校从A地购买x米2的草皮（x取整数），因路程关系，甲校从A地购买的草皮数不超过甲校从B地购买的草皮数，乙校从B地购买的草皮数大于甲校从B地购买的草皮数的
| 1 |
| 5 |
（3）在（2）的条件下，请你设计出总运费最低的草皮运送方案，并说明理由．
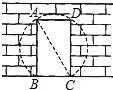（2012•新昌县模拟）为美化校园，学校决定将花园边墙上的矩形门ABCD改为以AC为直径的圆弧形门，如图所示，量得矩形门宽为1m，对角线AC的长为2m．
