题目内容
【题目】在平面直角坐标系中,函数![]() 的图象记为
的图象记为![]() ,函数
,函数![]() 的图象记为
的图象记为![]() ,其中
,其中![]() 为常数.图象
为常数.图象![]() ,
,![]() 合起来得到的图象记为
合起来得到的图象记为![]() .
.
(1)当![]() 时,
时,
①点![]() 在图象
在图象![]() 上,求
上,求![]() 的值;
的值;
②求图象![]() 与
与![]() 轴的交点坐标;
轴的交点坐标;
(2)当图象![]() 的最低点到
的最低点到![]() 轴距离为
轴距离为![]() 时,求
时,求![]() 的值;
的值;
(3)已知线段![]() 的两个端点坐标分别为
的两个端点坐标分别为![]() ,
,![]() ,当图象
,当图象![]() 与线段
与线段![]() 有两个交点时,直接写出
有两个交点时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)①![]() ;②交点坐标
;②交点坐标![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)①将a=2代入函数,求出函数解析式,再将点P代入即可解答;
②分两种情况分析,当x>2时和当![]() 时,分别解方程即可;
时,分别解方程即可;
(2)分两种情况,![]() 时以及
时以及![]() 时,分别画出图象,确定M2何时取最低点,再列出方程解答即可;
时,分别画出图象,确定M2何时取最低点,再列出方程解答即可;
(3)当![]() ,可分两种情况,分别画出图形,结合图形列出不等式;
,可分两种情况,分别画出图形,结合图形列出不等式;![]() ,画出图形,根据题意,结合图形,列出不等式即可解答.
,画出图形,根据题意,结合图形,列出不等式即可解答.
(1)①![]() 时,函数
时,函数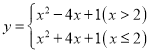 .
.
![]() 在图象上,代入
在图象上,代入![]() 中,得
中,得![]() ;
;
②当x>2时,![]() ,
,![]() ,
,![]() (舍)
(舍)
当![]() 时,
时,![]() 时,
时,![]() ,
,![]()
综上,交点坐标为![]() ,
,![]() ,
,![]() .
.
(2)![]() 时,图象如下所示,
时,图象如下所示,
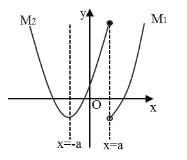
当![]() 时,
时,![]() 取最低点
取最低点
即![]() (方程无解),或
(方程无解),或![]()
解得![]() ,
,![]() (舍去).
(舍去).
![]() 时,图象如下所示,
时,图象如下所示,
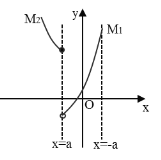
即![]() 时,
时,![]() 取最低点
取最低点
即![]() 或
或![]() (方程无解)
(方程无解)
![]() ,
,![]() (舍)
(舍)
综上,![]() 或
或![]() .
.
(3)①![]() ,如图所示,
,如图所示,
即![]() 代入
代入![]() 得
得![]() ,解得:
,解得:![]() .
.
![]() 代入
代入![]() 得
得![]() ,解得:
,解得:![]()
![]() 代入
代入![]() 得
得![]() ,解得:
,解得:![]() .
.
即![]() .
.
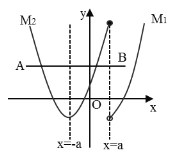
②![]() ,如下图所示,
,如下图所示,
即![]() 代入
代入![]() 得
得![]() ,解得:
,解得:![]() .
.
![]() 代入
代入![]() 得
得![]() ,解得:
,解得:![]()
![]() 代入
代入![]() 得
得![]() ,解得:
,解得:![]() .
.
即![]() .
.

③![]() ,如下图所示,
,如下图所示,
即![]() 代入
代入![]() 得
得![]() ,解得
,解得![]() .
.
![]() 代入
代入![]() 得
得![]() ,解得
,解得![]()
![]() 代入
代入![]() 得
得![]() ,解得
,解得![]() .
.
即![]() .
.
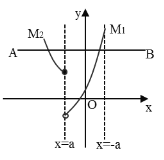
综上所述,![]() 或
或![]() .
.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案【题目】某中学开展黄梅戏演唱比赛,组委会将本次比赛的成绩(单位:分)进行整理,并绘制成如下频数分布表和频数分布直方图(不完整).
成绩 | 频数 | 频率 |
| 2 | 0.04 |
|
| 0.16 |
| 20 | 0.40 |
| 16 | 0.32 |
| 4 |
|
合计 | 50 | 1 |
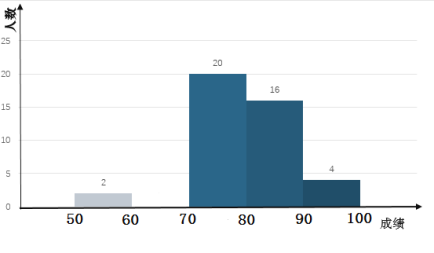
请你根据图表提供的信息,解答下列问题:
(1)求出![]() ,
,![]() 的值并补全频数分布直方图.
的值并补全频数分布直方图.
(2)将此次比赛成绩分为三组:![]() ;
;![]() ;
;![]() 若按照这样的分组方式绘制扇形统计图,则其中
若按照这样的分组方式绘制扇形统计图,则其中![]() 组所在扇形的圆心角的度数是多少?
组所在扇形的圆心角的度数是多少?
(3)学校准备从不低于90分的参赛选手中任选2人参加市级黄梅戏演唱比赛,求都取得了95分的小欣和小怡同时被选上的概率.