��Ŀ����
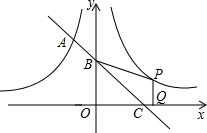 ��ͼ��һ�κ�����ͼ���뷴��������y1=-
��ͼ��һ�κ�����ͼ���뷴��������y1=- | 3 |
| x |
��1����һ�κ����Ľ���ʽ��
��2���躯��y2=
| a |
| x |
| 3 |
| x |
| a |
| x |
��������1������x��-1ʱ��һ�κ���ֵ���ڷ���������ֵ����x��-1ʱ��һ�κ���ֵС�ڷ���������ֵ�õ���A�����꣬���ô���ϵ���������Ľ���ʽ���ɣ�
��2�����B�����������P������꣬���ø��ߵ��ı��ε�����õ�������ϵʽ��õ�P�����꼴�ɣ�
��2�����B�����������P������꣬���ø��ߵ��ı��ε�����õ�������ϵʽ��õ�P�����꼴�ɣ�
����⣺��1����x��-1ʱ��һ�κ���ֵ���ڷ���������ֵ����x��-1ʱ��һ�κ���ֵС�ڷ���������ֵ��
��A��������-1��
��A��-1��3����
��һ�κ����Ľ���ʽΪy=kx+b����ֱ�߹�A��C��
��
��
��֮��
��
��һ�κ����Ľ���ʽΪy=-x+2��
��2����y2=
��ͼ����y1=-
(x��0)��ͼ�����y��Գƣ�
��y2=
��x��0����
��B����ֱ��y=-x+2��y��Ľ��㣬
��B��0��2����
��p��n��
��n��2��
S�ı���BCQP=S�ı���OQPB-S��OBC=2��
��
��2+
��n-
��2��2=2��
n=
��
��P��
��
����
��A��������-1��
��A��-1��3����
��һ�κ����Ľ���ʽΪy=kx+b����ֱ�߹�A��C��
��
|
��֮��
|
��һ�κ����Ľ���ʽΪy=-x+2��
��2����y2=
| a |
| x |
| 3 |
| x |
��y2=
| 3 |
| x |
��B����ֱ��y=-x+2��y��Ľ��㣬
��B��0��2����
��p��n��
| 3 |
| n |
S�ı���BCQP=S�ı���OQPB-S��OBC=2��
��
| 1 |
| 2 |
| 3 |
| n |
| 1 |
| 2 |
n=
| 5 |
| 2 |
��P��
| 5 |
| 2 |
| 6 |
| 5 |
������������Ҫ���鷴�������������ʣ�ע��ͨ���ⷽ��������������꣮ͬʱҪע���������ν�ϵ�˼�룮

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ����֪����������y=
��ͼ����֪����������y=
 ���
���
