Question

【题目】如图，∠1=∠2，∠3=∠4，∠5=∠6．求证：ED∥FB．在下面的括号中填上推理依据．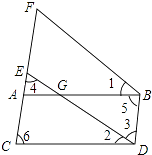

证明：∵∠3=∠4（ 已知 ）
∴CF∥BD
∴∠5+∠CAB=180°
∵∠5=∠6（ 已知 ）
∴∠6+∠CAB=180°（ 等式的性质 ）
∴AB∥CD
∴∠2=∠EGA
∵∠1=∠2（ 已知 ）
∴∠1=∠EGA（ 等量代换 ）
∴ED∥FB ．

Answer 1

【答案】内错角相等，两直线平行；两直线平行，同旁内角互补；同旁内角互补，两直线平行；两直线平行，同位角相等；同位角相等，两直线平行
【解析】证明：∵∠3=∠4（已知），

∴CF∥BD（内错角相等，两直线平行），

∴∠5+∠CAB=180°（两直线平行，同旁内角互补）．

∵∠5=∠6（已知），

∴∠6+∠CAB=180°（等式的性质），

∴AB∥CD（同旁内角互补，两直线平行），

∴∠2=∠EGA（两直线平行，同位角相等）．

∵∠1=∠2（已知），

∴∠1=∠EGA（等量代换），

∴ED∥FB（同位角相等，两直线平行）．

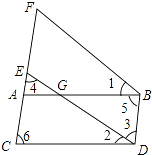
所以答案是：内错角相等，两直线平行；两直线平行，同旁内角互补；同旁内角互补，两直线平行；两直线平行，同位角相等；同位角相等，两直线平行．

【考点精析】利用平行线的判定与性质对题目进行判断即可得到答案，需要熟知由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质．