题目内容
【题目】如图所示,在Rt△ABC中,∠C=90°,∠BAC、∠ABC的平分线相交于点D,且DE⊥BC于点E,DF⊥AC于点F,那么四边形CEDF是正方形吗?请说明理由(提示:可作DG⊥AB于点G)
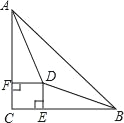
【答案】四边形CEDF为正方形,理由见解析
【解析】
过D作DG垂直AB于点G,由三个角为直角的四边形为矩形得到四边形CEDF为矩形,由AD为角平分线,利用角平分线定理得到DG=DF,同理得到DE=DG,等量代换得到DE=DF,利用邻边相等的矩形为正方形即可得证.
证明:如图,
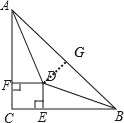
过D作DG⊥AB,交AB于点G,
∵∠C=∠DEC=∠DFC=90°,
∴四边形CEDF为矩形,
∵AD平分∠CAB,DF⊥AC,DG⊥AB,
∴DF=DG;
∵BD平分∠ABC,DG⊥AB,DE⊥BC,
∴DE=DG,
∴DE=DF,
∴四边形CEDF为正方形.

练习册系列答案
相关题目
【题目】某公司有2位股东,20名工人、从2006年至2008年,公司每年股东的总利润和每年工人的工资总额如图所示.
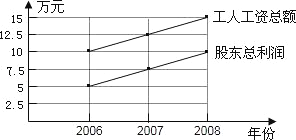
(1)填写下表:
年份 | 2006年 | 2007年 | 2008年 |
工人的平均工资/元 | 5000 | ||
股东的平均利润/元 | 25000 |
(2)假设在以后的若干年中,每年工人的工资和股东的利润都按上图中的速度增长,那么到哪一年,股东的平均利润是工人的平均工资的8倍?