题目内容
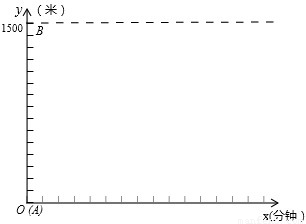
A、B两地相距1500米，甲、乙两人同时从A地出发到B地，甲步行的速度为100米/分钟，乙骑自行车的速度为300米/分钟，乙出发2分钟后自行车出现了故障，修车用了5分钟，然后继续以原速前往B地，设距A地的路程为y（米）和行进的时间为x（分钟）．（1）请你在给定的直角坐标系中，画出甲、乙两人y与x的函数图象；
（2）求两人在途中相遇的时间和距A地的路程（不包括A、B两地）
【答案】分析：（1）由题意可知甲的函数为y=100x，乙的函数为：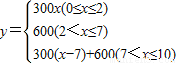
，根据函数可画出图象．
解答：解：（1）函数图象为：
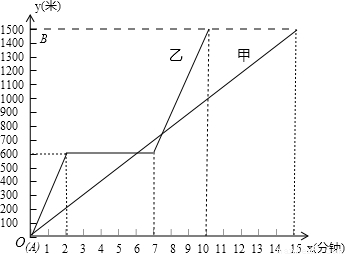
（2）第一次在途中相遇为：
100x=600，
x=6（分）．
第二次在途中相遇为：
100x=300（x-7）+600，
x=7.5（分）．
故两人在途中相遇的时间分别为6分和7.5分，距A地的路程分别为600米和750米．
点评：本题考查的是用一次函数解决实际问题，此类题是近年中考中的热点问题．注意利用一次函数求最值时，关键是应用一次函数的性质．
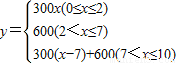，根据函数可画出图象．解答：解：（1）函数图象为：
（2）第一次在途中相遇为：
100x=600，
x=6（分）．
第二次在途中相遇为：
100x=300（x-7）+600，
x=7.5（分）．
故两人在途中相遇的时间分别为6分和7.5分，距A地的路程分别为600米和750米．
点评：本题考查的是用一次函数解决实际问题，此类题是近年中考中的热点问题．注意利用一次函数求最值时，关键是应用一次函数的性质．
练习册系列答案
相关题目
