题目内容
已知等腰梯形的底角为60°，上底长为2，上、下底长之比为1：3，那么梯形的面积为（ ）
A、8
| ||
B、4
| ||
C、8
| ||
D、4
|
分析：根据题意画出图形，然后可求出上底及下底的长，利用三角关系求出高后即可得出答案．
解答：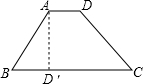
解：过点A作AD′BC于点D′，
由题意得：∠ABD=60°，AB=2，
又AB：BC=1：3，
故可得：BC=6，
∴BD=
（BC-AB）=2，
∴AD=BD′tan60°=2
，
面积=
（AB+BC）•AD=8
．
故选A．
解：过点A作AD′BC于点D′，由题意得：∠ABD=60°，AB=2，
又AB：BC=1：3，
故可得：BC=6，
∴BD=
| 1 |
| 2 |
∴AD=BD′tan60°=2
| 3 |
面积=
| 1 |
| 2 |
| 3 |
故选A．
点评：本题考查梯形面积的求法，难度不大，关键是利用三角关系求出高．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知等腰梯形的底角为45°，高为2，上底为2，则其面积为（ ）
| A、2 | B、6 | C、8 | D、12 |
已知等腰梯形的底角为45°，梯形的高等于上底，且下底的长为9，那么梯形的腰长为（ ）
| A、3 | ||
| B、5 | ||
C、3
| ||
D、2
|