Question

已知等腰梯形的底角为45°，高为2，上底为2，则其面积为（　　）

• A、2
• B、6
• C、8
• D、12

Answer 1

分析：根据底角为45°，过上底顶点作高可以得到等腰直角三角形，求出下底边的长，再代入梯形的面积公式即可求出面积．

解答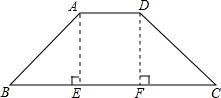：解：如图，分别过A、D作AE⊥BC，DF⊥BC，垂足为E、F，
则△ABE≌△DCF，AD=EF=2．
在直角△ABE中，∠B=45°
∴BE=AE=2，
∴在等腰梯形ABCD中，BE=FC=AE=2，
∵AD∥BC，AE⊥BC，DF⊥BC，
∴ADFE为矩形，
∴EF=AD=2，
∴BC=2BE+EF=4+2=6，
S_梯形=

1

2

×（2+6）×2=8．
故选C．

点评：考查梯形的面积公式的应用以及梯形的性质，过上底顶点作梯形的高是解决梯形问题常用的辅助线之一．