题目内容
已知|a-b-1|与(b-2014)2互为相反数,求代数式a2-2ab+b2的值.
1.
试题分析:因为|a-b-1|与(b-2014)2互为相反数,所以|a-b-1|+(b-2014)2=0,从而可求出a、b的值,代入代数式中去即可.
试题解析:∵|a-b-1|+(b-2014)2=0
∴a-b-1=0,b-2014=0
∴a=2015,b=2014,
当a=2015,b=2014时
a2-2ab+b2=(a-b)2=(2015-2014)2=1.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
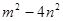 (2)、
(2)、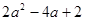








 (n=1,2,3,),记b1=2(1-a1),b2=2(1-a1)(1-a2),,bn=2(1-a1)(1-a2)(1-an),则通过计算推测出bn的表达式bn= .(用含n的代数式表示).
(n=1,2,3,),记b1=2(1-a1),b2=2(1-a1)(1-a2),,bn=2(1-a1)(1-a2)(1-an),则通过计算推测出bn的表达式bn= .(用含n的代数式表示). ,
, ,则
,则 的值是( )
的值是( )



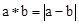 ,其中
,其中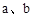 为实数,则
为实数,则 .
.