题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°, ![]() ,CM是斜边AB的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A=.
,CM是斜边AB的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A=.
【答案】30°
【解析】在Rt△ABC中,∠A<∠B 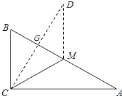
∵CM是斜边AB上的中线,
∴CM=AM,
∴∠A=∠ACM,
将△ACM沿直线CM折叠,点A落在点D处
设∠A=∠ACM=∠MCD=x度,
∴∠A+∠ACM=∠CMB,
∴∠CMB=2x,
如果CD恰好与AB垂直,垂足为G,
在Rt△CMG中,
∠MCG+∠CMB=90°
即3x=90°
x=30°
得到∠A=30°
故答案为 :30°.
根据直角三角形斜边上的中线等于斜边的一半即可得出CM=AM,根据等边对等角得出∠A=∠ACM,根据折叠的性质得出∠A=∠ACM=∠MCD=x度,根据三角形的外角定理得出∠A+∠ACM=∠CMB,即∠CMB=2x,根据直角三角形两锐角互余得出∠MCG+∠CMB=90°,从而列出关于x的方程,求解得出x的值,从而得出答案。

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目


