题目内容
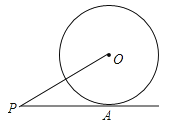
【题目】如图,射线PA切⊙O于点A,连接PO.
(1)在PO的上方作射线PC,使∠OPC=∠OPA(用尺规在原图中作,保留痕迹,不写作法),并证明PC是⊙O的切线;
(2)在(1)的条件下,若PC切⊙O于点B,AB=AP=4,求![]() 的长.
的长.
【答案】(1)作图见试题解析,证明见试题解析;(2)![]() .
.
【解析】
试题分析:(1)按照作一个角等于已知角的作图方法作图即可,连接OA,作OB⊥PC,由角平分线的性质证明OA=OB即可证明PC是⊙O的切线;
(2)先证明△PAB是等边三角形,则∠APB=60°,进而∠POA=60°,在Rt△AOP中求出OA,用弧长公式计算即可.
试题解析:(1)作图如右图,连接OA,过O作OB⊥PC,∵PA切⊙O于点A,∴OA⊥PA,又∵∠OPC=∠OPA,OB⊥PC,∴OA=OB,即d=r,∴PC是⊙O的切线;
(2)∵PA、PC是⊙O的切线,∴PA=PB,又∵AB=AP=4,∴△PAB是等边三角形,∴∠APB=60°,∴∠AOB=120°,∠POA=60°,在Rt△AOP中,tan60°=![]() ,∴OA=
,∴OA=![]() ,∴
,∴ =
=![]() .
.


练习册系列答案
相关题目
【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表: 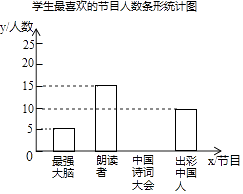
学生最喜爱的节目人数统计表
节目 | 人数(名) | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 | b% |
中国诗词大会 | a | 40% |
出彩中国人 | 10 | 20% |
根据以上提供的信息,解答下列问题:
(1)x= , a= , b=;
(2)补全上面的条形统计图;
(3)若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.