题目内容
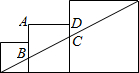 已知三个边长分别为1,2,3的正方形如图排成一排,图中四边形ABCD的周长是
已知三个边长分别为1,2,3的正方形如图排成一排,图中四边形ABCD的周长是| 7 |
| 2 |
| ||
| 2 |
| 7 |
| 2 |
| ||
| 2 |
分析:先由三个正方形的边长分别为1,2,3可知,AB=1,FD=1,AD=3,HG=1+2=3,GM=3,由FG∥MN可知CG是△HMN的中位线,故CG=
MN=
,进而可得出CD的长,连接BC,过点C作CE⊥AB于点E,可得出BE及CE的长,利用勾股定理可求出BC的长,进而得出结论.
| 1 |
| 2 |
| 3 |
| 2 |
解答: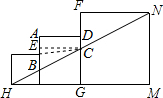 解:∵三个正方形的边长分别为1,2,3,
解:∵三个正方形的边长分别为1,2,3,
∴AB=1,FD=1,AD=2,HG=1+2=3,GM=3,
∵FG∥MN,
∴CG是△HMN的中位线,
∴CG=
MN=
,
∴CD=3-DF-CG=3-1-
=
,
连接BC,过点C作CE⊥AB于点E,
∵AB=1,CD=
,AD=2,
∴BE=AB-CD=1-
=
,
在Rt△BCE中,BC=
=
=
,
∴四边形ABCD的周长=AB+BC+CD+AD=1+
+
+2=
+
.
 解:∵三个正方形的边长分别为1,2,3,
解:∵三个正方形的边长分别为1,2,3,∴AB=1,FD=1,AD=2,HG=1+2=3,GM=3,
∵FG∥MN,
∴CG是△HMN的中位线,
∴CG=
| 1 |
| 2 |
| 3 |
| 2 |
∴CD=3-DF-CG=3-1-
| 3 |
| 2 |
| 1 |
| 2 |
连接BC,过点C作CE⊥AB于点E,
∵AB=1,CD=
| 1 |
| 2 |
∴BE=AB-CD=1-
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△BCE中,BC=
| CE2+BE2 |
22+(
|
| ||
| 2 |
∴四边形ABCD的周长=AB+BC+CD+AD=1+
| 17 |
| 1 |
| 2 |
| 7 |
| 2 |
| ||
| 2 |
点评:本题考查的是勾股定理、中位线定理及正方形的性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
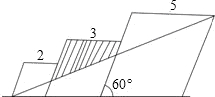 已知三个边长分别为2,3,5的三个菱形如图排列,菱形的较小锐角为60°,则图中阴影部分的面积为( )
已知三个边长分别为2,3,5的三个菱形如图排列,菱形的较小锐角为60°,则图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
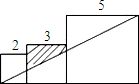 已知三个边长分别为2,3,5的正方形如图排列,则图中阴影部分面积为( )
已知三个边长分别为2,3,5的正方形如图排列,则图中阴影部分面积为( )| A、3.15 | B、3.75 | C、4 | D、4.35 |
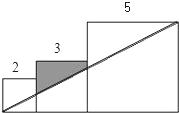 已知三个边长分别为2、3、5的正方形如图排列,则图中阴影部分面积为
已知三个边长分别为2、3、5的正方形如图排列,则图中阴影部分面积为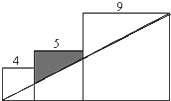 已知三个边长分别为4、5、9的正方形如图排列,则图中阴影部分面积为
已知三个边长分别为4、5、9的正方形如图排列,则图中阴影部分面积为