题目内容
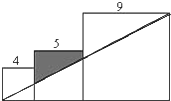 已知三个边长分别为4、5、9的正方形如图排列,则图中阴影部分面积为
已知三个边长分别为4、5、9的正方形如图排列,则图中阴影部分面积为| 35 |
| 4 |
| 35 |
| 4 |
分析:如图所示,阴影部分的面积=S正方形BCQW-S梯形VBFC,根据已知求得梯形的面积后,不难求得阴影部分的面积了.
解答: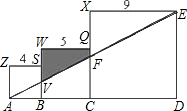 解:∵VB∥ED,三个正方形的边长分别为4、5、9,
解:∵VB∥ED,三个正方形的边长分别为4、5、9,
∴VB:DE=AB:AD,即VB:9=4:(4+5+9)=2:9,
∴VB=2;
∵CF∥ED,
∴CF:DE=AC:AD,即CF:9=9:18=1:2,
∴CF=
,
∵S梯形VBFC=
(BV+CF)•BC=
,
∴阴影部分的面积=S正方形BCQW-S梯形VBFC=
.
故答案为:
.
 解:∵VB∥ED,三个正方形的边长分别为4、5、9,
解:∵VB∥ED,三个正方形的边长分别为4、5、9,∴VB:DE=AB:AD,即VB:9=4:(4+5+9)=2:9,
∴VB=2;
∵CF∥ED,
∴CF:DE=AC:AD,即CF:9=9:18=1:2,
∴CF=
| 9 |
| 2 |
∵S梯形VBFC=
| 1 |
| 2 |
| 65 |
| 4 |
∴阴影部分的面积=S正方形BCQW-S梯形VBFC=
| 35 |
| 4 |
故答案为:
| 35 |
| 4 |
点评:本题考查了面积及等积转换.本题利用平行线分线段成比例的性质,正方形的性质求解.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
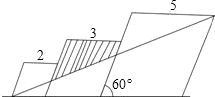 已知三个边长分别为2,3,5的三个菱形如图排列,菱形的较小锐角为60°,则图中阴影部分的面积为( )
已知三个边长分别为2,3,5的三个菱形如图排列,菱形的较小锐角为60°,则图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知三个边长分别为2,3,5的正方形如图排列,则图中阴影部分面积为( )
已知三个边长分别为2,3,5的正方形如图排列,则图中阴影部分面积为( )| A、3.15 | B、3.75 | C、4 | D、4.35 |
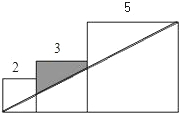 已知三个边长分别为2、3、5的正方形如图排列,则图中阴影部分面积为
已知三个边长分别为2、3、5的正方形如图排列,则图中阴影部分面积为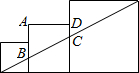 已知三个边长分别为1,2,3的正方形如图排成一排,图中四边形ABCD的周长是
已知三个边长分别为1,2,3的正方形如图排成一排,图中四边形ABCD的周长是