题目内容
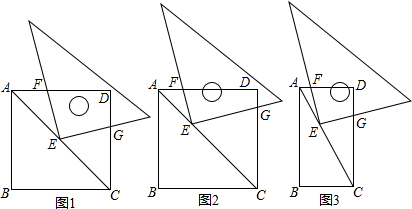
(2013•本溪三模)已知,AC是正方形ABCD的对角线,一个直角三角尺按如图所示方式放置,该三角尺的直角顶点E始终在AC上,一条直角边与AD相交于点F,另一条直角边与CD交于点G.
(1)如图1,当点E是AC的中点时,猜想EF与EG的数量关系并说明理由.
(2)①如图2,把(1)中的三角尺沿CA方向平移,当点E是AC的三等分点时,猜想EF与EG的数量关系并说明理由.
②图2中的正方形改为矩形,如图3,其他条件不变.①中的结论还成立吗?如果成立,请证明.如果不成立,请直接写出当∠ACD=30°时,EF与EG的数量关系.
(1)如图1,当点E是AC的中点时,猜想EF与EG的数量关系并说明理由.
(2)①如图2,把(1)中的三角尺沿CA方向平移,当点E是AC的三等分点时,猜想EF与EG的数量关系并说明理由.
②图2中的正方形改为矩形,如图3,其他条件不变.①中的结论还成立吗?如果成立,请证明.如果不成立,请直接写出当∠ACD=30°时,EF与EG的数量关系.

分析:(1)如图1,连接ED,根据正方形的性质证明△AFE≌△DGE,就可以得出EF=EG;
(2)如图2,作EM⊥AD于M,EN⊥CD于N,可以得出四边形MEND是矩形,就有EN=MD,由正方形的性质可以得出EM=AM,通过证明△EMF∽△ENG就可以得出结论;
(3)如图3,作EM⊥AD于M,EN⊥CD于N,可以得出四边形MEND是矩形,但EM≠AM,由△EMF∽△ENG就有
=
≠
,当∠ACD=30°时,EM=
CD,设AM=a,则EM=
a,MD=EG=2a,CD=3
a,就可以求出结论.
(2)如图2,作EM⊥AD于M,EN⊥CD于N,可以得出四边形MEND是矩形,就有EN=MD,由正方形的性质可以得出EM=AM,通过证明△EMF∽△ENG就可以得出结论;
(3)如图3,作EM⊥AD于M,EN⊥CD于N,可以得出四边形MEND是矩形,但EM≠AM,由△EMF∽△ENG就有
| EF |
| EG |
| EM |
| EN |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 3 |
解答: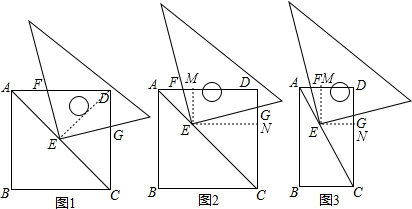 解:(1)EF=EG
解:(1)EF=EG
理由:如图1,连接ED.
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,∠FAE=45°.
∵E是AC的中点,
∴ED=AE=
AC,∠EDG=45°,∠AED=90°.
∴∠FAE=∠GDE.
∵∠FEG=90°,
∴∠AEF=∠DEG.
在△AFE和△DGE中,
,
∴△AFE≌△DGE(ASA),
∴EF=EG.
(2)EF=
EG
理由:如图2,作EM⊥AD于M,EN⊥CD于N,
∴∠EMD=∠EMA=∠EGD=90°.
∴EM∥CD.
∵∠D=90°,
∴四边形MEND是矩形,
∴MD=EN.
∵∠EAF=45°,
∴∠AEM=45°,
∴∠EAF=∠AEM,
∴AM=EM.
∵E是AC的三等分点,
∴
=
.
∵EM∥CD,
∴
=
=
.
∴
=
∵∠FEM+∠MEG=∠FEG=90°,∠MEG+∠GEN=90°,
∴∠FEM=∠GEN.
∵∠EMF=∠ENG,
∴△EFM∽△EGN,
∴
=
=
,
∴EF=
EG;
(3)如图3,作EM⊥AD于M,EN⊥CD于N,
∴∠EMD=∠EMA=∠EGD=90°.
∴EM∥CD.
∵∠D=90°,
∴四边形MEND是矩形,
∴MD=EN.
∵E是AC的三等分点,
∴
=
.
∵EM∥CD,
∴
=
=
.
∵EM≠AM,
∴
≠
,
∴
≠
.
∵∠FEM+∠MEG=∠FEG=90°,∠MEG+∠GEN=90°,
∴∠FEM=∠GEN.
∵∠EMF=∠ENG,
∴△EFM∽△EGN,
∴
=
,
∴
≠
,
故①的结论不成立;
当∠ACD=30°时,EF=
EG.
理由:
∵E是AC的三等分点,
∴
=
.
∵EM∥CD,
∴∠AEM=∠ACD=30°,
=
=
.
∴AE=2AM,
设AM=a,
∴AE=2a,MD=2a,
由勾股定理,得
EM=
a,MD=EG=2a,CD=3
a,
∴MD=EN=2a.
∵∠FEM+∠MEG=∠FEG=90°,∠MEG+∠GEN=90°,
∴∠FEM=∠GEN.
∵∠EMF=∠ENG,
∴△EFM∽△EGN,
∴
=
,
∴
=
=
,
∴EF=
EG.
 解:(1)EF=EG
解:(1)EF=EG理由:如图1,连接ED.
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,∠FAE=45°.
∵E是AC的中点,
∴ED=AE=
| 1 |
| 2 |
∴∠FAE=∠GDE.
∵∠FEG=90°,
∴∠AEF=∠DEG.
在△AFE和△DGE中,
|
∴△AFE≌△DGE(ASA),
∴EF=EG.
(2)EF=
| 1 |
| 2 |
理由:如图2,作EM⊥AD于M,EN⊥CD于N,
∴∠EMD=∠EMA=∠EGD=90°.
∴EM∥CD.
∵∠D=90°,
∴四边形MEND是矩形,
∴MD=EN.
∵∠EAF=45°,
∴∠AEM=45°,
∴∠EAF=∠AEM,
∴AM=EM.
∵E是AC的三等分点,
∴
| AE |
| CE |
| 1 |
| 2 |
∵EM∥CD,
∴
| AM |
| MD |
| AE |
| EC |
| 1 |
| 2 |
∴
| EM |
| EN |
| 1 |
| 2 |
∵∠FEM+∠MEG=∠FEG=90°,∠MEG+∠GEN=90°,
∴∠FEM=∠GEN.
∵∠EMF=∠ENG,
∴△EFM∽△EGN,
∴
| EF |
| EG |
| EM |
| EN |
| 1 |
| 2 |
∴EF=
| 1 |
| 2 |
(3)如图3,作EM⊥AD于M,EN⊥CD于N,
∴∠EMD=∠EMA=∠EGD=90°.
∴EM∥CD.
∵∠D=90°,
∴四边形MEND是矩形,
∴MD=EN.
∵E是AC的三等分点,
∴
| AE |
| CE |
| 1 |
| 2 |
∵EM∥CD,
∴
| AM |
| MD |
| AE |
| EC |
| 1 |
| 2 |
∵EM≠AM,
∴
| EM |
| EN |
| AE |
| EC |
∴
| EM |
| EN |
| 1 |
| 2 |
∵∠FEM+∠MEG=∠FEG=90°,∠MEG+∠GEN=90°,
∴∠FEM=∠GEN.
∵∠EMF=∠ENG,
∴△EFM∽△EGN,
∴
| EF |
| EG |
| EM |
| EN |
∴
| EF |
| EG |
| 1 |
| 2 |
故①的结论不成立;
当∠ACD=30°时,EF=
| ||
| 2 |
理由:
∵E是AC的三等分点,
∴
| AE |
| CE |
| 1 |
| 2 |
∵EM∥CD,
∴∠AEM=∠ACD=30°,
| AM |
| MD |
| AE |
| EC |
| 1 |
| 2 |
∴AE=2AM,
设AM=a,
∴AE=2a,MD=2a,
由勾股定理,得
EM=
| 3 |
| 3 |
∴MD=EN=2a.
∵∠FEM+∠MEG=∠FEG=90°,∠MEG+∠GEN=90°,
∴∠FEM=∠GEN.
∵∠EMF=∠ENG,
∴△EFM∽△EGN,
∴
| EF |
| EG |
| EM |
| EN |
∴
| EF |
| FG |
| ||
| 2a |
| ||
| 2 |
∴EF=
| ||
| 2 |
点评:本题考查了正方形的性质的运用,等腰直角三角形的性质的运用,全等三角形的判定及性质的运用,相似三角形的判定及性质的运用,直角三角形的性质的运用,矩形的判定及性质的运用,勾股定理的运用,平行线分线段成比例的运用,解答时证明三角形相似是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•本溪三模)房地产开发商在宣传介绍它的房屋室内结构时,发给客户有关的宣传单.下面的房间结构图是我们所说的( )视图.
(2013•本溪三模)房地产开发商在宣传介绍它的房屋室内结构时,发给客户有关的宣传单.下面的房间结构图是我们所说的( )视图.