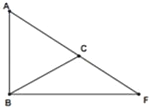
题目内容
【题目】在△ABF中,C为AF上一点且AB=AC.
(1)尺规作图:作出以AB为直径的⊙O,⊙O分别交AC、BC于点D、E,在图上标出D、E,在图上标出D、E(保留作图痕迹,不写作法).
(2)若∠BAF=2∠CBF,求证:直线BF是⊙O的切线;
(3)在(2)中,若AB=5,sin∠CBF=![]() ,求BC和BF的长.
,求BC和BF的长.
【答案】(1)作图见解析;(2)证明见解析;(3)BC=2![]() ,BF=
,BF=![]() .
.
【解析】试题分析:(1)作AB的垂直平分线交AB于O,以O为圆心,OA为半径作圆,⊙O即为所求;
(2)根据圆周角定理得到∠AEB=90°,根据等腰三角形的性质得到∠1=![]() ∠CAB,等量代换得到∠1=∠CBF,求出∠CBF+∠2=90°,然后,根据切线的判定即可得到结论;
∠CAB,等量代换得到∠1=∠CBF,求出∠CBF+∠2=90°,然后,根据切线的判定即可得到结论;
(3)根据已知条件得到sin∠1=![]() ,求出BE=ABsin∠1=
,求出BE=ABsin∠1=![]() ,根据勾股定理得到BC=2BE=2
,根据勾股定理得到BC=2BE=2![]() ,由勾股定理得AE=
,由勾股定理得AE=![]() =2
=2![]() ,于是得到sin∠2=
,于是得到sin∠2=![]() ,cos∠2=
,cos∠2=![]() ,根据三角函数的定义得到AG=3,根据相似三角形的性质即可得到结论.
,根据三角函数的定义得到AG=3,根据相似三角形的性质即可得到结论.
试题解析:(1)如图1,所示⊙O为所求作的圆;
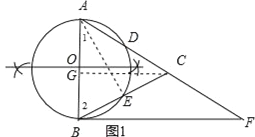
(2)连结AE,
∵AB是⊙O的直径,∴∠AEB=90°,∴∠1+∠2=90°,
∵AB=AC,∴∠1=![]() ∠CAB,
∠CAB,
∵∠BAF=2∠CBF,∴∠CBF=![]() CAB,∴∠1=∠CBF,∴∠CBF+∠2=90°,
CAB,∴∠1=∠CBF,∴∠CBF+∠2=90°,
∵即∠ABF=90°,∵AB是⊙O的直径,
∴直线BF是⊙O的切线;
(3)过点C作CG⊥AB于点G,
∵sin∠CBF=![]() ,∠1=∠CBF,∴sin∠1=
,∠1=∠CBF,∴sin∠1=![]() ,
,
∵∠AEB=90°,AB=5,∴BE=ABsin∠1=![]() ,
,
∵AB=AC,∠AEB=90°,∴BC=2BE=2![]() ,
,
在Rt△ABE中,由勾股定理得AE=![]() =2
=2![]() ,∴sin∠2=
,∴sin∠2=![]() ,cos∠2=
,cos∠2=![]() ,
,
在Rt△CBG中,GC=BC sin∠2=2![]() ×
×![]() =4,GB=BCcos∠2=2,∴AG=3,
=4,GB=BCcos∠2=2,∴AG=3,
∵GC∥BF,∴△AGC∽△ABF,∴![]() ,∴BF=
,∴BF=![]() =
=![]() .
.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案