题目内容
小明在复习数学知识时,针对“求一元二次方程的解”整理了以下几种方法,请你将有关内容补充完整:例题:求一元二次方程x2-x-1=0的两个解.
(1)解法一:选择合适的一种方法(公式法、配方法、分解因式法).
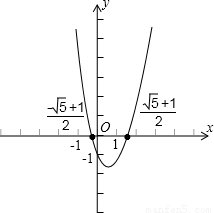
(2)解法二:利用二次函数图象与两坐标轴的交点求解.
如图,把方程x2-x-1=0的解看成是二次函数y=______的图象与x轴交点的横坐标即x1,x2就是方程的解.
(3)解法三:利用两个函数图象的交点求解①把方程x2-x-1=0的解看成是二次函数y=______的图象与一个一次函数y=______的图象交点的横坐标②画出这两个函数的图象,用x1,x2在x轴上标出方程的解.

【答案】分析:(1)用配方法解答一元二次方程;
(2)二次函数方程为y=ax2+bx+c与x轴交点的横坐标就是方程x2-x-1=0的解,所以,只要求出方程x2-x-1=0的根,就可以求出二次函数方程为y=ax2+bx+c与x轴交点;
(3)由(1)(2)解得x1、x2,再根据题意画出图象.
解答:解:(1)由原方程,得:
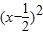
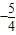 =0,即
=0,即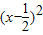 =
= ;
;
解得x1=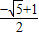 ,x2=
,x2= .
.
(2)设二次函数方程为y=ax2+bx+c(a,b,c均为实数,且a≠0).
由图象得知,该函数过点(0,-1),所以该点满足方程y=ax2+bx+c,
∴把(0,-1)代入方程y=ax2+bx+c,得c=-1,①
二次函数方程为y=ax2+bx+c与x轴交点的横坐标就是方程x2-x-1=0的解;
∴x1•x2= =-1,即c=-a;②
=-1,即c=-a;②
x1+x2=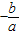 =1;③
=1;③
由①②③,得:
 ;
;
∴二次函数方程为y=x2-x-1.
(3)
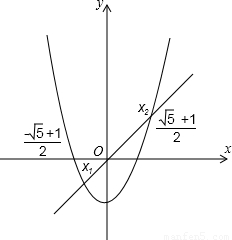
点评:本题考查的是二次函数与一元二次方程,在解答过程中,注意二次函数与一元二次方程之间的联系,并从中择取有用信息解题.
(2)二次函数方程为y=ax2+bx+c与x轴交点的横坐标就是方程x2-x-1=0的解,所以,只要求出方程x2-x-1=0的根,就可以求出二次函数方程为y=ax2+bx+c与x轴交点;
(3)由(1)(2)解得x1、x2,再根据题意画出图象.
解答:解:(1)由原方程,得:
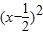
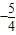 =0,即
=0,即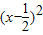 =
= ;
;解得x1=
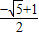 ,x2=
,x2= .
.(2)设二次函数方程为y=ax2+bx+c(a,b,c均为实数,且a≠0).
由图象得知,该函数过点(0,-1),所以该点满足方程y=ax2+bx+c,
∴把(0,-1)代入方程y=ax2+bx+c,得c=-1,①
二次函数方程为y=ax2+bx+c与x轴交点的横坐标就是方程x2-x-1=0的解;
∴x1•x2=
 =-1,即c=-a;②
=-1,即c=-a;②x1+x2=
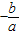 =1;③
=1;③由①②③,得:
 ;
;∴二次函数方程为y=x2-x-1.
(3)


点评:本题考查的是二次函数与一元二次方程,在解答过程中,注意二次函数与一元二次方程之间的联系,并从中择取有用信息解题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
小明在复习数学知识时,针对“求一元二次方程的解”,整理了以下的几种方法,请你按有关内容补充完整:
| 复习日记卡片 |
| 内容:一元二次方程解法归纳 时间:2007年6月×日 |
| 举例:求一元二次方程x2-x-1=0的两个解 |
| 方法一:选择合适的一种方法(公式法、配方法、分解因式法)求解 解方程:x2-x-1=0. 解: |
方法二:利用二次函数图象与坐标轴的交点求解如图所示,把方程x2-x-1=0的解看成是二次函数y= 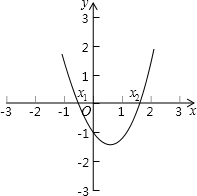 |
方法三:利用两个函数图象的交点求解 (1)把方程x2-x-1=0的解看成是一个二次函数y= (2)画出这两个函数的图象,用x1,x2在x轴上标出方程的解.  |
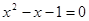 的两个解。
的两个解。 __________的图象与
__________的图象与 轴交点的横坐标,即
轴交点的横坐标,即 ,
, 就是方程的解。
就是方程的解。
 的两个解。
的两个解。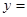 __________的图象与
__________的图象与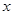 轴交点的横坐标,即
轴交点的横坐标,即 ,
, 就是方程的解。
就是方程的解。
