题目内容
如图所示，AB∥ED，∠B=48°，∠D=42°，BC垂直于CD吗？判断BC与CD的位置关系？并对你判断的结论加以证明．考点：平行线的性质,垂线
专题：几何图形问题,证明题
分析：根据两直线平行，内错角相等可得∠BCF=∠B，∠DCF=∠D，然后求出∠BCD=∠B+∠D，再根据垂直的定义解答；
根据两直线平行，同旁内角互补求出∠BCG，∠DCG，再根据周角等于360°求出∠BCD，然后根据垂直的定义解答．
根据两直线平行，同旁内角互补求出∠BCG，∠DCG，再根据周角等于360°求出∠BCD，然后根据垂直的定义解答．
解答：解：过点C作CF∥AB，
∵AB∥ED，
∴AB∥CF∥ED，
∴∠BCF=∠B，∠DCF=∠D，
∴∠BCD=∠B+∠D，
=48°+42°，
=90°，
∴BC⊥CD；
过点C作CG∥AB，
∵AB∥ED，
∴AB∥CG∥ED，
∴∠BCG=180°-∠B=180°-48°=132°，
∠DCG=∠D=180°-∠D=180°-42°=138°，
∴∠BCD=360°-∠BCG-∠DCG，
=360°-132°-138°，
=90°，
∴BC⊥CD．
∵AB∥ED，
∴AB∥CF∥ED，
∴∠BCF=∠B，∠DCF=∠D，
∴∠BCD=∠B+∠D，
=48°+42°，
=90°，
∴BC⊥CD；
过点C作CG∥AB，
∵AB∥ED，
∴AB∥CG∥ED，
∴∠BCG=180°-∠B=180°-48°=132°，
∠DCG=∠D=180°-∠D=180°-42°=138°，
∴∠BCD=360°-∠BCG-∠DCG，
=360°-132°-138°，
=90°，
∴BC⊥CD．
点评：本题考查了平行线的性质，熟记性质并作出辅助线是解题的关键，此类题目，难点在于过拐点作平行线．
练习册系列答案
阅读快车系列答案
相关题目
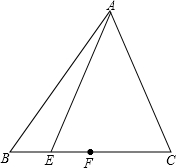数学课上，神奇而有魔力的黄金分割点激起了同学们极大的兴趣，某学习兴趣小组在探究该知识时，由黄金分割点联想到黄金分割线，类似的给出定义：直线AB将一个面积为S的图形分成两部分，这两部分的面积分别为S1和S2，如果S1：S2=S1：S（S1＞S2），那么称直线AB为该图的黄金分割线．
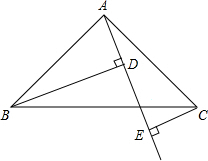如图，在Rt△ABC中，∠BAC=90°，AB=AC，AE是过A点的一条直线，且B点和C点在AE的两侧，BD⊥AE于点D，CE⊥AE于点E，CE=2，BD=6，求DE的长．
如图，已知⊙O1、⊙O2外切于点P，AB是一条外公切线，A、B为切点．