题目内容
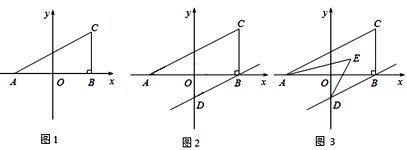
【题目】如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足![]() ,过C作
,过C作![]() 轴于B,
轴于B,
(1)求a,b的值;
(2)在y轴上是否存在点P,使得△ABC和△OCP的面积相等,若存在,求出点P坐标,若不存在,试说明理由.
(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,图3,
①求:∠CAB+∠ODB的度数;
②求:∠AED的度数.
【答案】(1)a=-2,b=2;(2)P(0,-4)或(0,4);(3)①∠CAB+∠ODB=90°;②∠AED=45°.
【解析】
(1)根据非负数的性质即可求得a、b的值;(2)先求得S△ABC=4,设P(0,t),根据S△OPC=![]() OP×2=
OP×2=![]() ×
×![]() ×2=4求得t值,即可求得点P的坐标;(3)①已知BD∥AC,根据两直线平行,内错角相等可得∠CAB=∠OBD,由∠OBD+∠ODB=90°,即可得∠CAB+∠ODB=90°;②根据角平分线的定义及①中的结论,可求得∠3+∠4=45°;过点E作EF∥AC,即可得EF∥BD∥AC,根据平行线的性质可得∠3=∠1,∠2=∠4,由此求得∠AED=∠1+∠2=∠4+∠3=45°.
×2=4求得t值,即可求得点P的坐标;(3)①已知BD∥AC,根据两直线平行,内错角相等可得∠CAB=∠OBD,由∠OBD+∠ODB=90°,即可得∠CAB+∠ODB=90°;②根据角平分线的定义及①中的结论,可求得∠3+∠4=45°;过点E作EF∥AC,即可得EF∥BD∥AC,根据平行线的性质可得∠3=∠1,∠2=∠4,由此求得∠AED=∠1+∠2=∠4+∠3=45°.
(1)∵![]() ,
,
∴a+2=0,b-2=0,
∴a=-2,b=2;
(2)∵a=-2,b=2,
∴A(-2,0),C(2,2),
∴S△ABC=![]() ABBC=
ABBC=![]() ×4×2=4;
×4×2=4;
设P(0,t),
∴S△OPC=![]() OP×2=
OP×2=![]() ×
×![]() ×2=
×2=![]() =4;
=4;
∴t=4或t=-4,
∴P(0,-4)或(0,4).
(3)①∵BD∥AC,
∴∠CAB=∠OBD,
∵∠OBD+∠ODB=90°,
∴∠CAB+∠ODB=90°;
②∵AE,DE分别平分∠CAB,∠ODB,
∴∠3=![]() ,∠4=
,∠4=![]() ,
,
∵∠CAB+∠ODB=90°,
∴∠3+∠4=![]() +
+![]() =45°,
=45°,
过点E作EF∥AC,

∵BD∥AC,
∴EF∥BD∥AC,
∴∠3=∠1,∠2=∠4,
∴∠AED=∠1+∠2=∠4+∠3=45°.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案