Question

【题目】如图，在△ABC中，∠ABC的平分线BE与∠ACB外角的平分线CE交于点E．

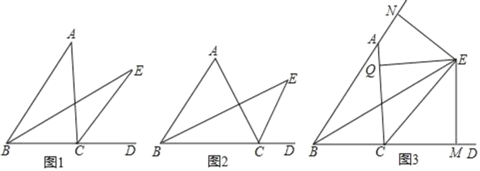
（1）如图1，若∠BAC＝40°，则∠BEC＝　 　°

（2）如图2，将∠BAC变为60°，则∠BEC＝　 　°，写出∠BAC与∠BEC的关系；并说明你的理由

（3）在图1的基础上过点E分别作EN⊥BA于N，EQ⊥AC于Q，EM⊥BD于M，如图3，

求证：△ANE≌AQE，并求出∠NAE的度数．

Answer 1

【答案】（1）20°；（2）30°， ∠E＝∠A，理由见解析；（3）见解析，∠NAE＝70°.

【解析】

（1）证明∠E＝∠A，即可解决问题；

（2）利用（1）中结论解决问题即可；

（3）连接AE．证明Rt△ANE≌Rt△AQE（HL）即可解决问题；

（1）依据三角形外角性质∠A＝∠ACD∠ABC，∠E＝∠ECD∠EBD

∵∠ABC的平分线与∠ACB外角的平分线交于点E，

∴∠EBD＝∠ABC，∠ECD＝∠ACD

∴∠E＝∠ECD∠EBD＝∠ACD∠ABC＝∠A＝20°．

（2）30°,∠E＝∠A

理由：∠A＝∠ACD﹣∠ABC，∠E＝∠ECD﹣∠EBD

∵∠ABC的平分线与∠ACB外角的平分线交于点E，

∴∠EBD＝∠ABC，∠ECD＝∠ACD

∴∠E＝∠ECD﹣∠EBD＝∠ACD﹣∠ABC＝∠A

（3）连接AE．

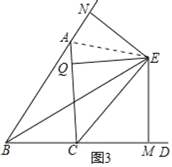
∵CE平分∠ACD，EQ⊥AC，EM⊥BD，

∴EQ＝EM，

同理EN＝EM

∴EN＝EQ，

在Rt△ANE和Rt△AQE中，

，

∴Rt△ANE≌Rt△AQE（HL），

∴∠EAQ＝∠EAN，

∵∠BAC＝40°，

∴∠NAQ＝140°，

∴∠NAE＝×140°＝70°