题目内容
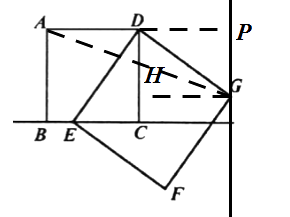
【题目】小明同学在做作业时,遇到如下问题:如图1,已知:等边△ABC,点D在BC上,以AD为边作等边△ADE,连接CE,求证:∠ACE=60°.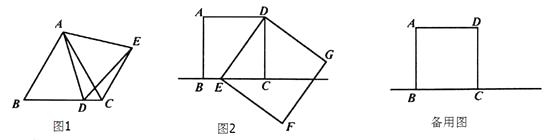
(1)请你解答小明的这道题;
(2)在这个问题中,当D在BC上运动时,点E是否在一条线段上运动?
(直接答“是”或“不是”)
(3)如图2,正方形ABCD的边长为2,E是直线BC上的一个动点,以DE为边作正方形DEFG(DEFG按逆时针排列)。当E在直线BC上运动时,点G是否在一条直线上运动?如果是,请你画出这条直线并证明;如果不是,也请说明理由;
(4)连接AG、CG,①求证:AG2-CE2是定值; ②求AG+CG的最小值(直接写出答案即可)。
【答案】
(1)
解:证明:∵△ABC和△ADE是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,∠B=60°,
∴∠BAD=∠CAE,∴△ABD△ACE,
∴∠ACE=∠B=60°.
(2)
解:是;∵∠ACE=60°,∠ACB=60°,∴∠BCE=120°,
∴E在以CB为一条边的120°角的另一边上,
当点D与B重合,E与C重合;
当点D与C重合时,CE的长最长=AC;
故点E在一条线段上运动。
(3)
解:是。证明:过G作GH⊥CD于H,∵四边形ABCD和四边形DEFG是正方形,
∴∠DCE=90°,∠EDG=90°,DE=DG,
∴∠EDC+∠GDC=90°,∠EDC+∠CED=90°,
∴∠GDC=∠CED,又∵DE=DG,∠DCE=∠GHD=90度,
∴△CDE△HGD,∴GH=CD=2.
又∵GH⊥CD,∴点G是在与CD的距离为2的直线上,过G作直线//CD,即点G在直线l上运动。
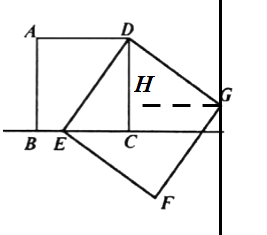
(4)
解:①延长AD交直线l于P,由(1)可得△CDE△HGD,
∴CE=DH。
∵l//CD,GH⊥CD,∴∠DHG=∠PGH=90°,
又∵∠PDH=90°,∴四边形DHGP是矩形,
∴PG=DH=CE,PD=GH=2,
在Rt△AGP中,AG2-PG2=AP2=42=16,
∴AG2-CE2=AG2-PG2=16是定值。
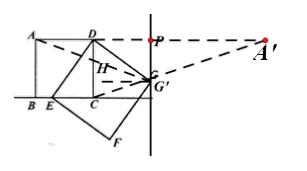
②过A作关于l的对称点A′,连接A′C,交直线l于G′,则AG+CG≥A′G′+CG′=A′C,
在Rt△A′CD中,CD=2,A′D=6,∴A′C = ![]() 。
。
【解析】(1)由△ABC和△ADE是等边三角形,可得AB=AC,AD=AE,∠BAC=∠DAE=60°,∠B=60°,则∠BAD=∠CAE,由“SAD”证得△ABD△ACE,即可证得∠ACE=∠B=60°;(2)在D的运动过程中∠BCE=∠ACE=+∠ACB=120°不变,CE边所在射线不变,且CE的最长=AC;(3)与前面同理,构造全等三角形,过G作GH⊥CD于H,证明△CDE△HGD,即GH=CD=2且GH⊥CD,则G在一条直线与CD平行,且距离为2;(4)①在(1)的结论下,延长AP交直线l于点P,则可得PG=DH=CE,则AG2-CE2=AG2-PG2是定值;②作A点关于直线l的对称点A’,连接A’C即为最短路径,再由勾股定理解出长度。
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.