题目内容
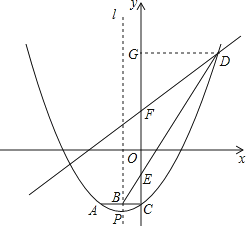
【题目】如图，抛物线y=ax2+bx﹣3交y轴于点C，直线l为抛物线的对称轴，点P在第三象限且为抛物线的顶点．P到x轴的距离为 
，到y轴的距离为1．点C关于直线l的对称点为A，连接AC交直线l于B． 
（1）求抛物线的表达式；
（2）直线y= 
x+m与抛物线在第一象限内交于点D，与y轴交于点F，连接BD交y轴于点E，且DE：BE=4：1．求直线y= x+m的表达式；
（3）若N为平面直角坐标系内的点，在直线y= x+m上是否存在点M，使得以点O、F、M、N为顶点的四边形是菱形？若存在，直接写出点M的坐标；若不存在，请说明理由．
【答案】
（1）
解：
∵抛物线y=ax2+bx﹣3交y轴于点C
∴C（0，﹣3）则 OC=3；
∵P到x轴的距离为 
，P到y轴的距离是1，且在第三象限，
∴P（﹣1，﹣ ）；
∵C关于直线l的对称点为A
∴A（﹣2，﹣3）；
将点A（﹣2，﹣3），P（﹣1，﹣ ）代入抛物线y=ax2+bx﹣3中，有：
，解得 
∴抛物线的表达式为y= 
x2+ 
x﹣3
（2）
解：过点D做DG⊥y 轴于G，则∠DGE=∠BCE=90°
∵∠DEG=∠BEC
∴△DEG∽△BEC
∵DE：BE=4：1，
∴DG：BC=4：1；
已知BC=1，则DG=4，点D的横坐标为4；
将x=4代入y= x2+ x﹣3中，得y=5，则 D（4，5）．
∵直线y= 
x+m过点D（4，5）
∴5= ×4+m，则 m=2；
∴所求直线的表达式y= x+2
（3）
解：由（2）的直线解析式知：F（0，2），OF=2；
设点M（x， x+2），则：OM2= 
x2+3x+4、FM2= x2；
（Ⅰ）当OF为菱形的对角线时，点M在线段OF的中垂线上，则点M的纵坐标为1；
∴ x+2=1，x=﹣ 
；即点M的坐标（﹣ ，1）．
（Ⅱ）当OF为菱形的边时，有：
①FM=OF=2，则： x2=4，x1= 
、x2=﹣
代入y= x+2中，得：y1= 
、y2= 
；
即点M的坐标（ ， ）或（﹣ ， ）；
②OM=OF=2，则： x2+3x+4=4，x1=0（舍）、x2=﹣ 
代入y= x+2中，得：y= 
；
即点M的坐标（﹣ ， ）；
综上，存在符合条件的点M，且坐标为（﹣ ，1）、（ ， ）、（﹣ ， ）、（﹣ ， ）
【解析】（1）已知点P到坐标轴的距离以及点P所在的象限，先确定点P的坐标；而点A、C关于抛物线对称轴对称，先求出点A的坐标，再由点A、P、C以及待定系数法确定二次函数的解析式．（2）过点D作y轴的垂线，通过构建的相似三角形先求出点D的横坐标，代入抛物线的解析式中能确定点D的坐标；再由待定系数法求直线DF的解析式．（3）由（2）的结论可先求出点F的坐标，先设出点M的坐标，则OF、OM、FM的表达式可求，若以O、F、M、N为顶点的四边形为菱形，那么可分两种情况：
①以OF为对角线，那么点M必为线段OF的中垂线与直线DF的交点，此时点M的纵坐标为点F纵坐标的一半，代入直线DF的解析式后可得点M的坐标；
②以OF为边，那么由OF=OM或FM=OF列出等式可求出点M的坐标．
