题目内容
【题目】已知四边形ABCD是正方形,点E、F分别在射线AB、射线BC上,AE=BF,DE与AF交于点O.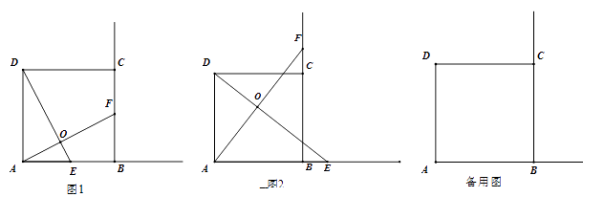
(1)如图1,当点E、F分别在线段AB、BC上时,则线段DE与线段AF的数量关系是 , 位置关系是.
(2)将线段AE沿AF进行平移至FG,连结DG.
①如图2,当点E在AB延长线上时,补全图形,写出AD,AE,DG之间的数量关系.
②若DG= ![]() ,
, ![]() ,直接写出AD长。
,直接写出AD长。
【答案】
(1)DE=AF;DE⊥AF
(2)
解:①如图2, DG2=2AD2+2AE
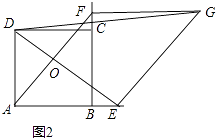
由题意得,AE=FG,AE∥FG,
∴四边形FAEG是平行四边形,
∴AF=EG,
由勾股定理得,DE2=AD2+AE2,
在△DAE和△ABF中,
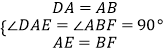 ,
,
∴△DAE≌△ABF,
∴DE=AF,DE⊥AF,
∴DE=EG,DE⊥EG,
∴DG2=2DE2,
∴DG2=2AD2+2AE2.
②由①得, ![]() ,
,
整理得AD2+AD-12=0
解得,AD1=3,AD2=-4(舍去).
故AD长为3.
【解析】解:(1)在△DAE和△ABF中,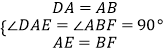
∴△DAE≌△ABF,
∴DE=AF,∠ADE=∠BAF,
∵∠ADE+∠AED=90°,
∴∠BAF+∠AED=90°,即∠AOE=90°,
∴DE⊥AF,
所以答案是:DE=AF;DE⊥AF.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目