题目内容
.已知圆锥主视图是边长为4的正三角形(即底面直径与母线长相等),则圆锥侧面积展开图扇形的圆心角为_________
由于圆锥主视图是边长为4的正三角形（即底面直径与母线长相等），由此得到圆锥的底面半径和母线长，而圆锥的侧面展开图是扇形，接着利用扇形的面积公式即可求解．
解：设圆锥侧面积展开图扇形的圆心角的度数为n，
∵圆锥主视图是边长为4的正三角形（即底面直径与母线长相等），
∴圆锥的底面半径和母线长分别是2和4，
∴S圆锥侧面积=
×2×2×π×4=
，
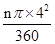∴n=180°．
故答案为：180°．
解：设圆锥侧面积展开图扇形的圆心角的度数为n，
∵圆锥主视图是边长为4的正三角形（即底面直径与母线长相等），
∴圆锥的底面半径和母线长分别是2和4，
∴S圆锥侧面积=
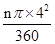×2×2×π×4=，∴n=180°．
故答案为：180°．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
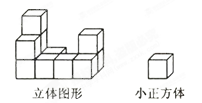
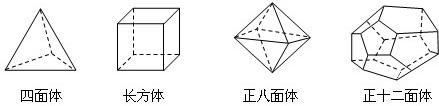
）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：
