��Ŀ����
������13�֣���ͼ12.1����֪�����߾�������ԭ��O��x������һ��E(4,0)������M������Ϊ (m,4)��ֱ������ABCD�Ķ���A���O�غϣ�AD��AB�ֱ���x�ᡢy���ϣ���BC=1��AD=2��AB=3.
��1����m��ֵ���������ߵĺ�����ϵʽ��
��2����ֱ������ABCD��ÿ��1����λ���ȵ��ٶȴ�ͼ12.1��ʾ��λ����x�������������ƽ���ƶ���ͬʱһ����PҲ����ͬ���ٶȴӵ�A�������B�����ƶ����������˶���ʱ��Ϊt��(0��t��3)��ֱ��AB��������ߵĽ���ΪN(��ͼ12.2��ʾ).
�ٵ�tΪ��ֵʱ����PNC����PNΪ�ױߵĵ��������Σ�
������P��N��C��DΪ����Ķ�������ΪS������S�Ƿ�������ֵ�������ڣ����������ֵ���������ڣ���˵ �����ɣ�
�����ɣ�
 |
��1������֪�����������ߵ���Գ��ԣ���m=2��
�� ����M������Ϊ(2,4)�� ������������(1��)
�ʿ������ϵʽΪy=a(x-2)2+4.
�������߾���O(0,0)�����ǵ�a(0-2)2+4=0����� a=-1. ������(3��)
�� ��������ϵʽΪy=-(x-2)2+4����y=-x2+4x. ������(4��)
��2���� �� ��A��x����������ϣ���N���������ϣ�CB��PN,
�� OA=AP=t��
�� ��P��B��N������ֱ�Ϊ(t,t)��(t,3)��(t, -t2+4t).
�� BP=3-t��AN= -t2+4t��0��t��3��.
�� PN=AN-AP=(-t2+4t)-t=-t2+3t=t(3-t)��0. ������(6��)
Ҫʹ�á�PNC����PNΪ�ױߵĵ��������Σ�
ֻ��PN=2BP����-t2+3t=2(3-t)��
��������t2-5t+6=0����� t1=2��t2=3.
��t=3ʱ��P��N�����غϣ����������⣬��ȥ.
�� ��t=2ʱ����PNC����PNΪ�ױߵĵ���������. ������(8��)
�� S�������ֵ. ������(9��)
��������PN=0����t=0��t=3ʱ���Ե�P��N��C��DΪ����Ķ������������.
��t=0����S=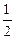 AD��AB=
AD��AB=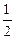 ��3��2=3.
��3��2=3.
��t=3����S=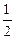 BC��AB=
BC��AB=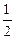 ��1��3=
��1��3=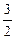 .
.
��������PN��0����0��t��3ʱ���Ե�P��N��C��DΪ����Ķ�������ı���. ����PD��CN����
����PD��CN����
S=S�ı���ANCD-S��ADP= S����ABCD+S��BCN -S��ADP
=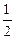 (BC+AD)��AB+
(BC+AD)��AB+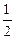 BN��BC-
BN��BC-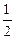 AP��AD
AP��AD
=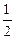 (1+2)��3+
(1+2)��3+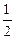 (-t2+4t- 3)��1-
(-t2+4t- 3)��1-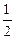 t��2
t��2
=-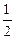 t2+t+ 3=-
t2+t+ 3=-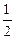 (t-1)2+
(t-1)2+ .
.
��-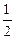 ��0��0��t��3����t=1ʱ��S���=
��0��0��t��3����t=1ʱ��S���= .
.
������������t=1ʱ���Ե�P��N��C��DΪ����Ķ������������ֵ��
������ֵΪ . ������������(13��)
. ������������(13��)
����

 ��У����ϵ�д�
��У����ϵ�д�

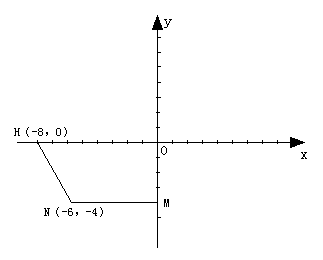
 ��
�� �ᡢ
�ᡢ ��ֱ��ڵ�B��C ��������
��ֱ��ڵ�B��C �������� ����B��C���㣬����
����B��C���㣬���� �ǣ�1�������������ϵ�һ�����㣬����P��ֱ��
�ǣ�1�������������ϵ�һ�����㣬����P��ֱ�� ���ڵ�M����ֱ��BC�ڵ�N ��
���ڵ�M����ֱ��BC�ڵ�N ��