题目内容
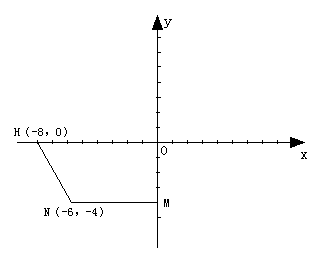
(本小题满分13分)如图,平面直角坐标系中有一直角梯形OMNH,点H的坐
标为(-8,0),点N的坐标为(-6,-4).
(1)画出直角梯形OMNH绕点O旋转180°的图形OABC,并写出顶点A,B,C的坐标(点M的对应点为A,点N的对应点为B,点H的对应点为C);
(2)求出过A,B,C三点的抛物线的表达式;
(3)截取CE=OF=AG=m,且E,F,G分别在线段CO,OA,AB上,求四边形BEFG的面积S与m之间的函数关系式,并写出自变量m的取值范围;面积S是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由;
(4)在(3)的情况下,四边形BEFG是否存在邻边相等的情况,若存在,请直接写出此时m的值,并指出相等的邻边;若不存在,说明理由.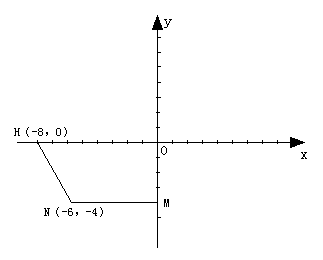
(1)利用中心对称性质,画出梯形OABC.……………1分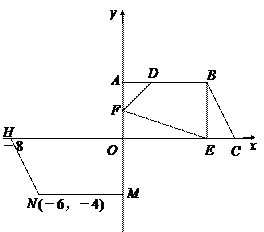
∵A,B,C三点与M,N,H分别关于点O中心对称,
∴A(0,4),B(6,4),C(8,0) ………………… 3分
(写错一个点的坐标扣1分)
(2)设过A,B,C三点的抛物线关系式为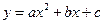 ,
,
∵抛物线过点A(0,4),
∴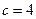 .则抛物线关系式为
.则抛物线关系式为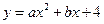 .
.
将B(6,4), C(8,0)两点坐标代入关系式,得 …………4分
…………4分
解得 …………5分
…………5分
所求抛物线关系式为: .·················· 6分
.·················· 6分
(3)∵OA=4,OC=8,∴AF=4-m,OE=8-m.················ 7分
∴
 OA(AB+OC)
OA(AB+OC)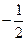 AF·AG
AF·AG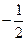 OE·OF
OE·OF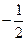 CE·OA
CE·OA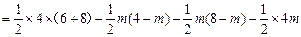
 ( 0<
( 0< <4)······················ 8分
<4)······················ 8分
∵ . ∴当
. ∴当 时,S的取最小值.
时,S的取最小值.
又∵0<m<4,∴不存在m值,使S的取得最小值. ······································· 10分
(4)当 时,GB=GF,当
时,GB=GF,当 时,BE=BG.··········· 13分
时,BE=BG.··········· 13分
解析

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
 (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为 ,短轴两个端点为.A、B且四边形
,短轴两个端点为.A、B且四边形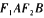 是边长为2的正方形.
是边长为2的正方形.
 为定值;
为定值; (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为 ,短轴两个端点为.A、B且四边形
,短轴两个端点为.A、B且四边形 是边长为2的正方形.
是边长为2的正方形.
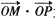 为定值;
为定值;