题目内容
如图,直角梯形ABCD中,AD∥BC,∠A=90°,∠C=60°,AD=3cm,BC=9cm.⊙O1的圆心O1从点A开始沿折线A-D-C以1cm/s的速度向点C运动,⊙O2的圆心O2从点B开 始沿BA边以
始沿BA边以
cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1,O2分别从点A、点B同时出发,运动的时间为ts.
(1)设经过t秒,⊙O2与腰CD相切于点F,过点F画EF⊥DC,交AB于E,则EF=______;
(2)过E画EG∥BC,交DC于G,画GH⊥BC,垂足为H.则∠FEG=______;
(3)求此时t的值;
(4)在0<t≤3范围内,当t为何值时,⊙O1与⊙O2外切?
 始沿BA边以
始沿BA边以| 3 |
(1)设经过t秒,⊙O2与腰CD相切于点F,过点F画EF⊥DC,交AB于E,则EF=______;
(2)过E画EG∥BC,交DC于G,画GH⊥BC,垂足为H.则∠FEG=______;
(3)求此时t的值;
(4)在0<t≤3范围内,当t为何值时,⊙O1与⊙O2外切?
(1)∵当⊙O2与腰CD相切时,EF的长为⊙O2的半径,
∴EF=4cm;
(2)∵∠CGH+∠EGF=90°,∠EGF+∠FEG=90°,
∴∠FEG=∠CGH,
在Rt△CGH中,∠C=60°,
∴∠CGH=30°,
∴∠FEG=30°;
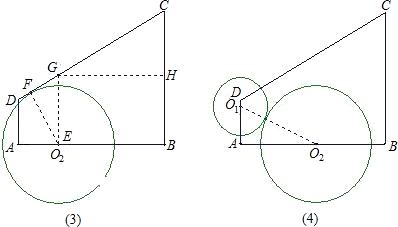
(3)设点O2运动到点E处时,⊙O2与腰CD相切.依题意画图,如图所示,
在直角△CGH中,∠C=60°,∠CGH=30°,GH=
t,
∴CH=t,BH=GE=9-t;
在Rt△EFG中,∠FEG=30°,EF=4,GE=9-t;
在Rt△EFG中,EF=GE×cos∠FEG,即:4=(9-t)×
;
∴t=(9-
)秒;
(4)由于0<t≤3,所以,点O1在边AD上,
如图所示,连接O1O2,由两圆外切可知O1O2=6cm;
AB=(BC-AD)×tan60°=6×
=6
,
∴O2A=6
-
t,
在Rt△O1O2A中,由勾股定理得:t2+(6
-
t)2=62,即t2-9t+18=0,
解得t1=3,t2=6(不合题意,舍去)
∴经过3秒,⊙O1与⊙O2外切.
故答案为:4cm;30°.
∴EF=4cm;
(2)∵∠CGH+∠EGF=90°,∠EGF+∠FEG=90°,
∴∠FEG=∠CGH,
在Rt△CGH中,∠C=60°,
∴∠CGH=30°,
∴∠FEG=30°;
(3)设点O2运动到点E处时,⊙O2与腰CD相切.依题意画图,如图所示,
在直角△CGH中,∠C=60°,∠CGH=30°,GH=
| 3 |
∴CH=t,BH=GE=9-t;
在Rt△EFG中,∠FEG=30°,EF=4,GE=9-t;
在Rt△EFG中,EF=GE×cos∠FEG,即:4=(9-t)×
| ||
| 2 |
∴t=(9-
8
| ||
| 3 |
(4)由于0<t≤3,所以,点O1在边AD上,
如图所示,连接O1O2,由两圆外切可知O1O2=6cm;
AB=(BC-AD)×tan60°=6×
| 3 |
| 3 |
∴O2A=6
| 3 |
| 3 |
在Rt△O1O2A中,由勾股定理得:t2+(6
| 3 |
| 3 |
解得t1=3,t2=6(不合题意,舍去)
∴经过3秒,⊙O1与⊙O2外切.
故答案为:4cm;30°.


练习册系列答案
相关题目







