题目内容
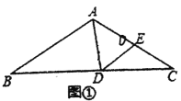
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 在
在![]() 所在的直线上,点
所在的直线上,点![]() 在射线
在射线![]() 上,且
上,且![]() ,连接
,连接![]() .
.
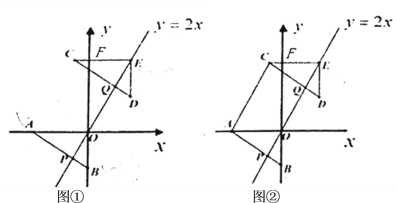
(1)如图①,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
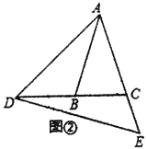
(2)如图②,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
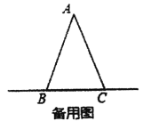
(3)当点![]() 在直线
在直线![]() 上(不与点
上(不与点![]() 、
、![]() 重合)运动时,试探究
重合)运动时,试探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)40°;(2)36°;(3)∠BAD与∠CDE的数量关系是2∠CDE=∠BAD.
【解析】
(1)根据等腰三角形的性质得到∠BAC=110°,根据等腰三角形的性质和三角形的外角的性质即可得到结论;
(2)根据三角形的外角的性质得到∠E=75°-18°=57°,根据等腰三角形的性质和三角形的外角的性质即可得到结论;
(3)设∠ABC=∠ACB=y°,∠ADE=∠AED=x°,∠CDE=α,∠BAD=β,分3种情况:①如图1,当点D在点B的左侧时,∠ADC=x°-α,②如图2,当点D在线段BC上时,∠ADC=y°+α,③如图3,当点D在点C右侧时,∠ADC=y°-α,根据这3种情况分别列方程组即,解方程组即可得到结论.
(1)∵∠B=∠C=35°,
∴∠BAC=110°,
∵∠BAD=80°,
∴∠DAE=30°,
∵AD=AE,
∴∠ADE=∠AED=75°,
∴∠CDE=∠AED-∠C=75°35°=40°;
(2)∵∠ACB=75°,∠CDE=18°,
∴∠E=75°18°=57°,
∴∠ADE=∠AED=57°,
∴∠ADC=39°,
∵∠ABC=∠ADB+∠DAB=75°,
∴∠BAD=36°.
(3)设∠ABC=∠ACB=y°,∠ADE=∠AED=x°,∠CDE=α,∠BAD=β
①如图1,当点D在点B的左侧时,∠ADC=x°﹣α
∴ ,①-②得,2α﹣β=0,
,①-②得,2α﹣β=0,
∴2α=β;
②如图2,当点D在线段BC上时,∠ADC=y°+α
∴ ,②-①得,α=β﹣α,
,②-①得,α=β﹣α,
∴2α=β;
③如图3,当点D在点C右侧时,∠ADC=y°﹣α
∴ ,②-①得,2α﹣β=0,
,②-①得,2α﹣β=0,
∴2α=β.
综上所述,∠BAD与∠CDE的数量关系是2∠CDE=∠BAD.