题目内容
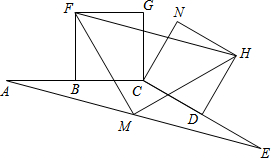 如图,在等腰△ACE中,已知CA=CE=2,AE=2c,点B、D、M分别是边AC、CE、AE的中点,以BC、CD为边长分别作正方形BCGF和CDHN,连结FM、FH、MH.
如图,在等腰△ACE中,已知CA=CE=2,AE=2c,点B、D、M分别是边AC、CE、AE的中点,以BC、CD为边长分别作正方形BCGF和CDHN,连结FM、FH、MH.(1)求△ACE的面积;
(2)试探究△FMH是否是等腰直角三角形?并对结论给予证明;
(3)当∠GCN=30°时,求△FMH的面积.
分析:(1)连结CM,在RT△ACM中,利用勾股定理求出CM的长即可求出△ACE的面积;
(2)△FMH是等腰直角三角形,连结BM,DM,首先证明四边形四边形BCDM是边长1的菱形,设∠A=α,则∠BMA=∠DME=∠E=∠A=α,∠MDC=2α.利用三角形的内角和证明∠FMH=180°-∠AMH-∠CMH=180°-(α+θ)=90°即可;
(3)作△HMD的边MD上的高HQ,则由勾股定理有求出DQ的长,再利用三角形的面积公式即可求出△FMH的面积.
(2)△FMH是等腰直角三角形,连结BM,DM,首先证明四边形四边形BCDM是边长1的菱形,设∠A=α,则∠BMA=∠DME=∠E=∠A=α,∠MDC=2α.利用三角形的内角和证明∠FMH=180°-∠AMH-∠CMH=180°-(α+θ)=90°即可;
(3)作△HMD的边MD上的高HQ,则由勾股定理有求出DQ的长,再利用三角形的面积公式即可求出△FMH的面积.
解答:解:(1)连结CM,
∵CA=CE=2,M分别是边AE的中点,
∴CM⊥AE.…(1分)
在RT△ACM中,AM=
AE=c,
由勾股定理得,CM=
=
.
∴S△ACE=
AE×CM=
.…(2分)
(2)△FMH是等腰直角三角形.…(3分)
证明:连结BM,DM.∵CA=CE=2,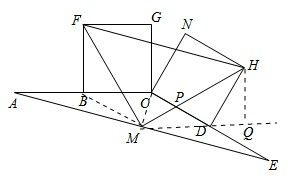
点B、D、M分别是边AC、CE、AE的中点,∴BC=CD=BM=DM=1.…(4分)
∴四边形BCDM是边长为1的菱形,
∴∠CBM=∠CDM.
∴∠CBM+∠FBC=∠CDM+∠HDC,即∠FBM=∠HDM,
∴△FBM≌△MDH.…(4分)
∴FM=MH,且∠FMB=∠HMD(设大小为θ).
又设∠A=α,则∠BMA=∠DME=∠E=∠A=α,∠MDC=2α.
在△MDH中,DM=DH=1,
∴∠DHM=∠DMH=θ,
由三角形内角和定理可有:∴∠DHM+∠DMH+∠MDH=180°,
得:θ+θ+2α+90°=180°,
∴α+θ=45°.…(5分)
∴∠FMH=180°-∠AMH-∠CMH=180°-(α+θ)=90°.
∴△FMH是等腰直角三角形. …(6分)
(3)在等腰△ACE中,∠ACE=180°-2α,
又当∠GCN=30°时,∠ACE=360°-∠GCN=180°-30°=150°
从而有:180°-2α=150°,又α+θ=45°,得θ=30°,α=15°.…(7分)
如图,作△HMD的边MD上的高HQ,则由勾股定理有:
DQ=
DH=
,HQ2=DH2-DQ2=12-(
)2=
MQ=1+
=
,MH2=MQ2+HQ2=
+
=3…(8分)
∴△FMH的面积S△FMH=
FM×HM=
HM2=
.…(9分)
∵CA=CE=2,M分别是边AE的中点,
∴CM⊥AE.…(1分)
在RT△ACM中,AM=
| 1 |
| 2 |
由勾股定理得,CM=
| AC2-AM2 |
| 4-c2 |
∴S△ACE=
| 1 |
| 2 |
| c |
| 2 |
| 4-c2 |
(2)△FMH是等腰直角三角形.…(3分)
证明:连结BM,DM.∵CA=CE=2,

点B、D、M分别是边AC、CE、AE的中点,∴BC=CD=BM=DM=1.…(4分)
∴四边形BCDM是边长为1的菱形,
∴∠CBM=∠CDM.
∴∠CBM+∠FBC=∠CDM+∠HDC,即∠FBM=∠HDM,
∴△FBM≌△MDH.…(4分)
∴FM=MH,且∠FMB=∠HMD(设大小为θ).
又设∠A=α,则∠BMA=∠DME=∠E=∠A=α,∠MDC=2α.
在△MDH中,DM=DH=1,
∴∠DHM=∠DMH=θ,
由三角形内角和定理可有:∴∠DHM+∠DMH+∠MDH=180°,
得:θ+θ+2α+90°=180°,
∴α+θ=45°.…(5分)
∴∠FMH=180°-∠AMH-∠CMH=180°-(α+θ)=90°.
∴△FMH是等腰直角三角形. …(6分)
(3)在等腰△ACE中,∠ACE=180°-2α,
又当∠GCN=30°时,∠ACE=360°-∠GCN=180°-30°=150°
从而有:180°-2α=150°,又α+θ=45°,得θ=30°,α=15°.…(7分)
如图,作△HMD的边MD上的高HQ,则由勾股定理有:
DQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 4 |
∴△FMH的面积S△FMH=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了勾股定理的运用、菱形的判定、等腰直角三角形的判定、三角形的内角和定理以及全等三角形的判定和性质,题目的综合性强难度大.解题的关键是作△HMD的边MD上的高HQ,构造直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
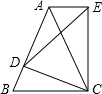 如图,在等腰△ABC中,AB=AC,D是AB上的动点,作等腰△EDC∽△ABC.
如图,在等腰△ABC中,AB=AC,D是AB上的动点,作等腰△EDC∽△ABC.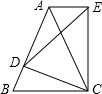 如图,在等腰△ABC中,AB=AC,D是AB上的动点,作等腰△EDC∽△ABC.
如图,在等腰△ABC中,AB=AC,D是AB上的动点,作等腰△EDC∽△ABC.