题目内容
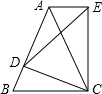如图，在等腰△ABC中，AB=AC，D是AB上的动点，作等腰△EDC∽△ABC．求证：（1）△ACE∽△BCD；
（2）AE∥BC．
分析：（1）由△EDC∽△ABC 可以得到
=
，∠ECD=∠ACB，接着得到∠ACE=∠BCD，利用相似三角形的判定得到△ACE∽△BCD；
（2）根据相似三角形的性质得到∠EAC=∠B，由AB=AC可以得到∠B=∠ACB，由此利用平行线的判定即可证明AE∥BC．
| BC |
| DC |
| AC |
| EC |
（2）根据相似三角形的性质得到∠EAC=∠B，由AB=AC可以得到∠B=∠ACB，由此利用平行线的判定即可证明AE∥BC．
解答：证明：（1）∵△EDC∽△ABC （1分）
∴
=
，∠ECD=∠ACB（2分）
∴∠ACE=∠BCD （1分）
∴△ACE∽△BCD（2分）；
（2）根据（1）得∠EAC=∠B（1分）
∵AB=AC （1分）
∴∠B=∠ACB （1分）
∴∠EAC=∠ACB （1分）
∴AE∥BC （2分）
∴
| BC |
| DC |
| AC |
| EC |
∴∠ACE=∠BCD （1分）
∴△ACE∽△BCD（2分）；
（2）根据（1）得∠EAC=∠B（1分）
∵AB=AC （1分）
∴∠B=∠ACB （1分）
∴∠EAC=∠ACB （1分）
∴AE∥BC （2分）
点评：此题主要考查了相似三角形的性质与判定，解题的关键是熟练运用相似三角形的性质与平顶尖级问题．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
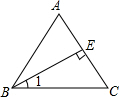如图，在等腰△ABC中，AB=AC，BE⊥AC，垂足为E，则∠1与∠A的关系式为（ ）| A、∠1=∠A | ||
B、∠1=
| ||
| C、∠1=2∠A | ||
| D、无法确定 |
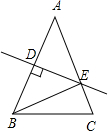如图，在等腰△ABC中，AB=AC，AB的垂直平分线DE交AB于点D，交另一腰AC于点E，若∠EBC=15°，则∠A=
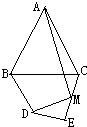24、如图，在等腰△ABC中，AB=AC，∠ABC=α，在四边形BDEC中，DB=DE，∠BDE=2α，M为CE的中点，连接AM，DM．
（2012•丽水）如图，在等腰△ABC中，AB=AC，∠BAC=50°．∠BAC的平分线与AB的中垂线交于点O，点C沿EF折叠后与点O重合，则∠CEF的度数是
如图，在等腰△ABC中，AB=AC=10cm，直线DE垂直平分AB，分别交AB、AC于D、E两点．若BC=8cm，则△BCE的周长是