题目内容
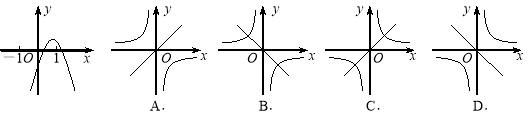
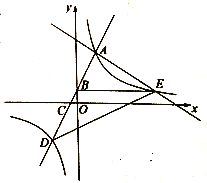
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于点
交于点![]() 、
、![]() ,直线
,直线![]() 交
交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() ,直线
,直线![]() 过点
过点![]() ,与双曲线
,与双曲线![]() 的另一个交点为点
的另一个交点为点![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() 的值为_____.
的值为_____.
【答案】![]()
【解析】
过点A作AF⊥y轴于点F,过点D作DG⊥y轴于点G,先联立直线AB反比例函数的解析式求出A、D点的横坐标,得到AF与DG,再由三角形的面积比与相似三角形的比例线段得到k与b的关系,进而用b的代数式表示A点坐标,再将其代入AE的解析式中,用b表示n,进而联立AE与反比例函数解析式求出E的坐标,最后根据已知三角形的面积,得到b的方程求得b,问题便可迎刃而解.
解:过点A作AF⊥y轴于点F,过点D作DG⊥y轴于点G,
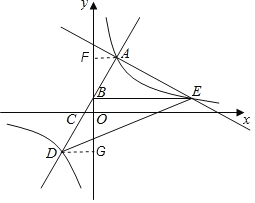
∴AF∥DG,
∴△ABF∽△DBG,
∴![]() ,
,
∵S△ABE:S△DBE=3:4,
∴![]() ,
,
由2x+b=![]() 得,2x2+bx﹣k=0,
得,2x2+bx﹣k=0,
解得,x=![]() ,
,
即A点的横坐标为![]() ,D点横坐标为
,D点横坐标为![]() ,
,
∴AF=![]() ,DG=
,DG=![]() =
=![]() ,
,
∴![]() ,
,
解得,k=6b2,
∴A点的横坐标为![]() =
=![]() b,纵坐标为
b,纵坐标为![]() =4b,
=4b,
∴A(![]() b,4b),
b,4b),
把A(![]() b,4b)代入y=﹣
b,4b)代入y=﹣![]() +n中,得n=5b,
+n中,得n=5b,
∴AE的解析式为:y=﹣![]() +5b,
+5b,
联立方程组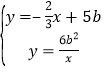 ,
,
解得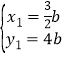 ,
,![]() ,
,
∴E(6b,b),
∵B(0,b),
∴BE∥x轴,
∴BE=6b,
∴![]() =
=![]() ,
,
∵S△ABE=4,
∴9b2=4,
∴b2=![]() ,
,
∴k=6b2=6×![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目