题目内容
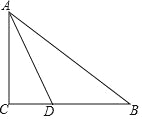
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是高线,
是高线,![]() ,
,![]() ,
,
(1)用直尺与圆规作三角形内角![]() 的平分线
的平分线![]() (不写作法,保留作图痕迹).
(不写作法,保留作图痕迹).
(2)在(1)的前提下,判断①![]() ,②
,②![]() 中哪一个正确?并说明理由.
中哪一个正确?并说明理由.

【答案】(1)见解析;(2)②对,证明见解析.
【解析】
(1)以点A为圆心,任意长为半径画弧,分别与AB,AC相交于一点,然后以这两点为圆心,大于这两点距离的一半画弧,两弧交于一点,连接交点与A的直线,与BC相交与点E,则AE为![]() 的平分线;
的平分线;
(2)由三角形内角和定理和角平分线定理,得到![]() ,由余角性质得到∠CAD=
,由余角性质得到∠CAD=![]() ,即可求出
,即可求出![]() .
.
解:(1)如图所示,AE为所求;

(2)②![]() 正确;
正确;
理由如下:∵![]() ,
,![]() ,
,
∴∠BAC=![]() ,
,
∵AE平分![]() ,
,
∴∠CAE=![]() ,
,
∵AD是高,
∴∠ADC=90°,
∴∠CAD=![]() ,
,
∴![]() ,
,
∴![]() ;
;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目