题目内容
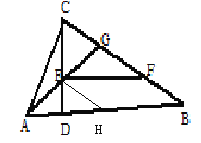
【题目】如图,已知:在Rt△ABC中,AC⊥BC,CD⊥AB于D,AG平分∠BAC,交BC于G,交CD于E,EF∥AB交BC于F,求证:CE=BF.

【答案】证明见解析
【解析】
试题分析:过点E作EH∥BC交AB于点H,则得到四边形EHBF是平行四边形,然后可证△ACE≌△AHE(AAS),然后可得证结论.
试题解析:过点E作EH∥BC交AB于点H,则四边形EHBF是平行四边形,EH=BF,
∵∠ACD+∠BCD=90°,∠DBC+∠BCD=90°,
∴∠ACD=∠DBC,又∵∠AHE=∠DBC,∴∠AHE=∠ACF,
在△ACE和△AHE中,∠AHE=∠ACF,
∠ACD=∠DBC
AE=AE
∴△ACE≌△AHE(AAS),∴EH=CE,又EH=BF,∴CE=BF

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
