题目内容
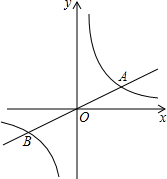 如图,已知直线y=
如图,已知直线y=| 1 |
| 2 |
| k |
| x |
(1)求k的值及点B的坐标;
(2)若双曲线y=
| k |
| x |
(3)若点P在坐标轴上,且△APB为等腰三角形,那么这样的P点有多少个?请你直接写出其中的一个点的坐标(不需要求解过程).
分析:(1)把A点的横坐标代入直线y=
x求出x的值即可得出A点坐标,再根据点A在反比例函数y=
上即可得出k的值;由于反比例函数及正比例函数的图象均关于原点对称即可得出B点坐标;
(2)先由点C的纵坐标为8求出C点坐标,分别过点C、A作CD⊥x轴,AE⊥x轴,连接OC,则S△AOC=S△OCD+S梯形AEDC-S△AOE,故可得出结论.
(3)若AP=BP则点P在线段AB的垂直平分线上,与点P在坐标轴上相矛盾,故此种情况不存在,再分点P在x轴上与y轴上两种情况进行讨论即可.
| 1 |
| 2 |
| k |
| x |
(2)先由点C的纵坐标为8求出C点坐标,分别过点C、A作CD⊥x轴,AE⊥x轴,连接OC,则S△AOC=S△OCD+S梯形AEDC-S△AOE,故可得出结论.
(3)若AP=BP则点P在线段AB的垂直平分线上,与点P在坐标轴上相矛盾,故此种情况不存在,再分点P在x轴上与y轴上两种情况进行讨论即可.
解答:解:(1)∵直线y=
x与双曲线y=
(k>0)交于A,B两点,且点A的横坐标为4,
∴y=
×4=2,
∴A(4,2),
∴k=4×2=8;
∵反比例函数及正比例函数的图象均关于原点对称,
∴A、B两点关于原点对称,
∴B(-4,-2);
(2) 如图,∵由(1)知k=8,
如图,∵由(1)知k=8,
∴反比例函数的解析式为:y=
,
∵C点的纵坐标为8,
∴8=
,解得x=1,
∴C(1,8),
分别过点C、A作CD⊥x轴,AE⊥x轴,连接OC,
∵A(4,2),C(1,8)
∴CD=8,AE=2,DE=4-1=3,
∴S△AOC=S△OCD+S梯形AEDC-S△AOE,即
×8+
(8+2)×3-
×8=15.
(3)8个;
∵A(4,2),B(-4,-2),
∴AB=
=4
,
当点P在x轴上时,设P(x,0),
若AP=AB,即
=4
,解得x=4±2
,
∴P1(4+2
,0),P2(4-2
,0);
当BP=AB时,
=4
,解得x=-4±2
,
∴P3(-4+2
,0),P4(-4-2
,0);
当点P在y轴上时,设P(0,y)
若AP=AB,即
=4
,解得y=±6,
∴P5(0,6),P6(0,-6);
若BP=AB,即
=4
,解得y=±10,
∴P7(0,10),P8(0,-10),
综上所述,P点坐标为:P(0,6)、(0,-10)、(-2
-4,0)、(-4+2
,0)、(4-2
,0)、(4+2
,0)、(0,-6)、(0,10).
| 1 |
| 2 |
| k |
| x |
∴y=
| 1 |
| 2 |
∴A(4,2),
∴k=4×2=8;
∵反比例函数及正比例函数的图象均关于原点对称,
∴A、B两点关于原点对称,
∴B(-4,-2);
(2)
 如图,∵由(1)知k=8,
如图,∵由(1)知k=8,∴反比例函数的解析式为:y=
| 8 |
| x |
∵C点的纵坐标为8,
∴8=
| 8 |
| x |
∴C(1,8),
分别过点C、A作CD⊥x轴,AE⊥x轴,连接OC,
∵A(4,2),C(1,8)
∴CD=8,AE=2,DE=4-1=3,
∴S△AOC=S△OCD+S梯形AEDC-S△AOE,即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)8个;
∵A(4,2),B(-4,-2),
∴AB=
| (4+4)2+(2+2)2 |
| 5 |
当点P在x轴上时,设P(x,0),
若AP=AB,即
| (4-x)2+22 |
| 5 |
| 19 |
∴P1(4+2
| 19 |
| 19 |
当BP=AB时,
| (x+4)2+22 |
| 5 |
| 19 |
∴P3(-4+2
| 19 |
| 19 |
当点P在y轴上时,设P(0,y)
若AP=AB,即
| 42+(2-y)2 |
| 5 |
∴P5(0,6),P6(0,-6);
若BP=AB,即
| 42+(y+2)2 |
| 5 |
∴P7(0,10),P8(0,-10),
综上所述,P点坐标为:P(0,6)、(0,-10)、(-2
| 19 |
| 19 |
| 19 |
| 19 |
点评:本题考查的是反比例函数综合题,涉及到反比例函数与一次函数的交点问题、三角形及梯形的面积公式、等腰三角形的性质等知识,在解答(3)时要注意进行分类讨论,不要漏解.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
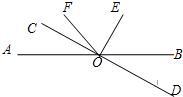 16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.
16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.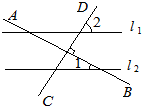 5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( )
5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( )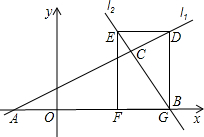 如图,已知直线l1:
如图,已知直线l1: (2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2=
(2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2=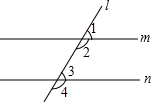 如图,已知直线m∥n,则下列结论成立的是( )
如图,已知直线m∥n,则下列结论成立的是( )