��Ŀ����
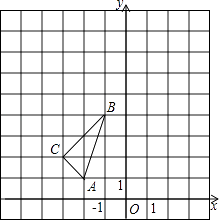
����Ŀ��������������ε������߶�Ӧ��ȣ��нǻ�������ô�����������ν������������Σ���ͼ2���ֱ��ԡ�ABC�ı�AB��ACΪ��������������ABDE��ACGF����ͼ�е����������ξ��ǻ��������Σ�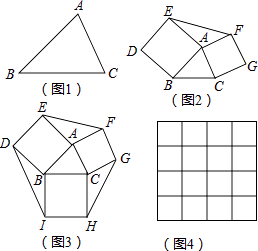
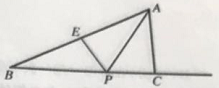
��1��ͼ1�еġ�ABC��BC������һ��D���߶�AD����ABC�ֳ��������������Σ����D��BC�ߵ�����
��2��֤����ͼ2�еġ�ABC�ָ���������������������ȣ�
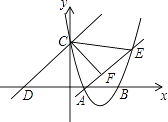
��3����ͼ3����ͼ2�Ļ���������BCΪ��������������BCHI����֪��������������ֱ���17��13��10����ͼ3��������DEFGHI�����Ϊ �� ����ʾ����������ͼ4�����ABC�������
���𰸡�
��1���е�
��2��
�⣺��ͼ2��ʾ��
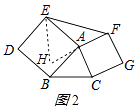
�ӳ�FA����H��ʹ��AH=AF��
����EH��
���ı���ABDE���ı���ACGF�������Σ�
��AB=AE��AF=AC����BAE=��CAF=90�㣬
���EAF+��BAC=180�㣬
���AEF�͡�ABC���������������Σ�
�ߡ�EAH+��HAB=��BAC+��HAB=90�㣬
���EAH=��BAC��
��AF=AC��
��AH=AB��
�ڡ�AEH�͡�ABC�У�  ��
��
���AEH�ա�ABC��
��S��AEF=S��AEH=S��ABC
��3��62
���������⣺��1.����ͼ1�У���BC���ϵ�����AD����ABD�͡�ADC�ǻ��������Σ�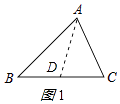
���Դ��ǣ��е㣮
��3.���߳�Ϊ ![]() ��
�� ![]() ��
�� ![]() ����������ͼ4��ʾ��
����������ͼ4��ʾ��
��S��ABC=3��4��2��1.5��3=5.5��
��S������=17+13+10+4��5.5=62��
���Դ��ǣ�62��
�����㾫����������Ҫ�����������ε������ȫ�������ε����ʵ����֪ʶ�㣬��Ҫ���������ε����=1/2���ס��ߣ�ȫ�������εĶ�Ӧ�����; ȫ�������εĶ�Ӧ����Ȳ�����ȷ�����⣮

 �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�