��Ŀ����
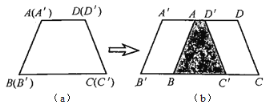
����Ŀ����ͼ��ʾ����λũ������һ��Ƭ��أ�����״ǡ����һ��ƽ���ı��Σ������ڶԽ���![]() ����һ��ˮ��
����һ��ˮ��![]() ��ũ��������ǰ���������������������ε����(��ͼ����Ӱ����)��С���ӣ�ʣ�µ�ȫ��������ӣ�����ˮ��
��ũ��������ǰ���������������������ε����(��ͼ����Ӱ����)��С���ӣ�ʣ�µ�ȫ��������ӣ�����ˮ��![]() �����������ӹ��ã�����ƽ���ı������߳���ͬ��������������֮��������������࣬���۷ף���Ϊ������䲻��ƽ����ô����Ϊ________��(���ƽ������ƽ��)������________��
�����������ӹ��ã�����ƽ���ı������߳���ͬ��������������֮��������������࣬���۷ף���Ϊ������䲻��ƽ����ô����Ϊ________��(���ƽ������ƽ��)������________��

���𰸡���ƽ ![]() ��
��![]() �����֮�͵���ƽ���ı���
�����֮�͵���ƽ���ı���![]() �������һ�룮
�������һ�룮
��������
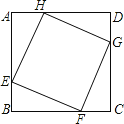
��E��GH��AD��AD��H����BC��G�����������ε������ʽ�����AED�͡�CEB�����֮�͵���![]() AD��GH���ٸ���ƽ���ı��ε������������𰸣�
AD��GH���ٸ���ƽ���ı��ε������������𰸣�
��ƽ��
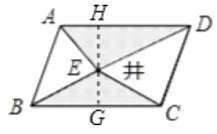
�����ǣ���E��GH��AD��AD��H����BC��G��
��ƽ���ı���ABCD��
AD��BC��AD��BC��
��GH��AD��
��GH��BC��
����Ӱ���ֵ������S��EAD��S��EBC��![]() AD��EH��
AD��EH��![]() BC��EG��
BC��EG��![]() AD��GH��
AD��GH��![]() Sƽ���ı���ABCD��
Sƽ���ı���ABCD��
���AED�͡�CEB�����֮�͵���ƽ���ı���ABCD�������һ�룬
�ʴ�Ϊ����ƽ����AED�͡�CEB�����֮�͵���ƽ���ı���ABCD�������һ�룮

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ