题目内容
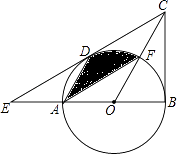
【题目】如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( ) 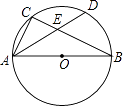
A.2.5
B.2.8
C.3
D.3.2
【答案】B
【解析】解:如图1,连接BD、CD, 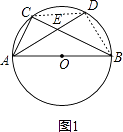 ,
,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴BD= ![]() ,
,
∵弦AD平分∠BAC,
∴CD=BD= ![]() ,
,
∴∠CBD=∠DAB,
在△ABD和△BED中,![]()
∴△ABD∽△BED,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
解得DE= ![]() ,
,
∴AE=AD﹣DE=5﹣ ![]() =2.8.
=2.8.
故选:B
【考点精析】本题主要考查了勾股定理的概念和圆周角定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
【题目】水果店以每箱60元新进一批苹果共400箱,为计算总重量,从中任选30箱苹果称重,发现每箱苹果重量都在10千克左右,现以10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,将称重记录如下:
规格 | ﹣0.2 | ﹣0.1 | 0 | 0.1 | 0.2 | 0.5 |
筐数 | 5 | 8 | 2 | 6 | 8 | 1 |
(1)求30箱苹果的总重量
(2)若每千克苹果的售价为10元,则卖完这批苹果共获利多少元
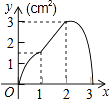
【题目】一位射击运动员在10次射击训练中,命中靶的环数如图. 请你根据图表,完成下列问题: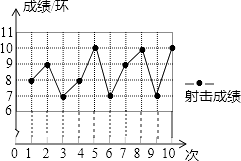
(1)补充完成下面成绩表单的填写:
射击序次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩/环 | 8 | 10 | 7 | 9 | 10 | 7 | 10 |
(2)求该运动员这10次射击训练的平均成绩.